- Review
- Open access
- Published:
Stochastic backgrounds of relic gravitons: a theoretical appraisal
PMC Physics A volume 4, Article number: 1 (2010)
Abstract
Stochastic backgrounds or relic gravitons, if ever detected, will constitute a prima facie evidence of physical processes taking place during the earliest stages of the evolution of the plasma. The essentials of the stochastic backgrounds of relic gravitons are hereby introduced and reviewed. The pivotal observables customarily employed to infer the properties of the relic gravitons are discussed both in the framework of the ΛCDM paradigm as well as in neighboring contexts. The complementarity between experiments measuring the polarization of the Cosmic Microwave Background (such as, for instance, WMAP, Capmap, Quad, Cbi, just to mention a few) and wide band interferometers (e.g. Virgo, Ligo, Geo, Tama) is emphasized. While the analysis of the microwave sky strongly constrains the low-frequency tail of the relic graviton spectrum, wide-band detectors are sensitive to much higher frequencies where the spectral energy density depends chiefly upon the (poorly known) rate of post-inflationary expansion.
PACS codes: 04.30.-w, 14.70.Kv, 04.80.Nn, 98.80.-k
1 The spectrum of the relic gravitons
1.1 The frequencies and wavelengths of relic gravitons
Terrestrial and satellite observations, scrutinizing the properties of the electromagnetic spectrum, are unable to test directly the evolution of the background geometry prior to photon decoupling. The redshift probed by Cosmic Microwave Background (CMB in what follows) observations is of the order of zdec ≃ 1087 and it roughly corresponds to the peak of the visibility function, i.e. when most of the CMB photons last scattered free electrons (and protons). After decoupling the ionization fraction drops; the photons follow null geodesics whose slight inhomogeneities can be directly connected with the fluctuations of the spatial curvature present before matter-radiation decoupling. It is appropriate to mention that the visibility function has also a second (smaller) peak which arises because the Universe is reionized at late times. The reionization peak affects the overall amplitude of the CMB anisotropies and polarization. It also affects the peak structure of the linear polarization. The present data suggest that the typical redshift for reionization is zreion ~11 and the corresponding optical depth is 0.087. The optical depth at reionization actually constitutes one of the parameters of the concordance model (see below Eq. (2.7)).
The temperature of CMB photons is, today, of the order of 2.725 K. The same temperature at photon decoupling must have been of the order of about 2962 K, i.e. 0.25 eV (natural units ħ = c = kB = 1 will be adopted; in this system, K = 8.617 × 10-5eV). The CMB temperature increases linearly with the redshift: this fact may be tested empirically by observing at high redshifts clouds of chemical compounds (like CN) whose excited levels may be populated thanks to the higher value of the CMB temperature [1, 2].
The initial conditions for the processes leading to formation of CMB anisotropies are set well before matter radiation equality and right after neutrino decoupling (taking place for temperatures of the order of the MeV) whose associated redshift is around 1010. The present knowledge of particle interactions up to energy scales of the order of 200 GeV certainly provides important (but still indirect) clues on the composition of the plasma.
If ever detected, relic gravitons might provide direct informations on the evolution of the Hubble rate for much higher redshifts. In a rudimentary realization of the ΛCDM paradigm, the inflationary phase can be modeled in terms of the expanding branch of de-Sitter space. Recall that, in the acronym ΛCDM, Λ qualifies the dark-energy component while CDM qualifies the dark matter component. Assuming that, right after inflation, the Universe evolves adiabatically and is dominated by radiation, the redshift associated with the end of inflation can be approximately computed as

where g ρ denotes the weighted number of relativistic degrees of freedom at the onset of the radiation dominated evolution and 106.75 corresponds to the value of the standard model of particle interactions. Fermions and bosons contribute with different factors to g ρ . By assuming that all the species of the standard model are in local thermodynamic equilibrium (for instance for temperature higher than the top quark mass), g ρ will be given by g ρ = 28 + (7/8)90 = 106.75 where 28 and 90 count, respectively, the bosonic and the fermionic contributions.
In Eq. (1.1) it has been also assumed that H ≃10-5 MP as implied by the CMB observations in the conventional case of single-field inflationary models. In the latter case, absent other paradigms for the generation of (adiabatic) curvature perturbations, the condition H ≃ 10-5 MP is required for reproducing correctly the amplitude of the temperature and polarization anisotropies of the CMB. For more accurate estimates the quasi-de Sitter nature of the inflationary expansion must be taken into account. In the ΛCDM paradigm, the basic mechanism responsible for the production of relic gravitons is the parametric excitation of the (tensor) modes of the background geometry and it is controlled by the rate of variation of space-time curvature.
In the present article the ΛCDM paradigm will always be assumed as a starting point for any supplementary considerations. The reasons for this choice are also practical since the experimental results must always be stated and presented in terms of a given reference model. Having said this, most of the considerations presented here can also be translated (with the appropriate computational effort) to different models.
Given a specific scenario for the evolution of the Universe (like the ΛCDM model), the relic graviton spectra can be computed. The amplitude of the relic graviton spectrum over different frequencies depends upon the specific evolution of the Hubble rate. The theoretical error on the amplitude increases with the frequency: it is more uncertain (even within a specified scenario) at high frequencies rather than at small frequencies.
The experimental data, at the moment, do not allow either to rule in or to rule out the presence of a primordial spectrum of relic gravitons compatible with the ΛCDM scenario. The typical frequency probed by CMB experiments is of the order of νp = kp/(2π) ≃ 10-18 Hz = 1 aHz where kp is the pivot frequency at which the tensor power spectra are assigned. We are here enforcing the usual terminology stemming from the prefixes of the International System of units: aHz (for atto Hz i.e. 10-18 Hz), fHz (for femto Hz, i.e. 10-15 Hz) and so on. CMB experiments will presumably set stronger bounds on the putative presence of a tensor background for frequencies  (aHz). This bound will be significant also for higher frequencies only if the whole post-inflationary thermal history is assumed to be known and specified.
(aHz). This bound will be significant also for higher frequencies only if the whole post-inflationary thermal history is assumed to be known and specified.
The typical frequency window of wide-band interferometers (such as Ligo and Virgo) is located between few Hz and 10 kHz, i.e. roughly speaking, 20 orders of magnitude larger than the frequency probed by CMB experiments. The typical frequency window of LISA (Laser Interferometric Space Antenna) extends down to 10-100 μHz. While Virgo and Ligo are now operating, the schedule of LISA is still under discussion. The frequency range of wide-band interferometers will be conventionally denoted by νLV. To compute the relic graviton spectrum over the latter range of frequencies, the evolution of our Universe should be known over a broad range of redshifts. We do have some plausible guesses on the evolution of the plasma from the epoch of neutrino decoupling down to the epoch of photon decoupling. The latter range of redshifts corresponds to an interval of comoving frequencies going from νp ≃ 10-18 Hz up to νbbn ≃ 0.01 nHz ~10-11Hz (at most).
In Fig. 1 (plot at the left) the frequency range of the relic graviton spectrum is illustrated, starting from the (comoving) frequency νp whose associated (comoving) wavelength is of the order of of 1026 m, i.e. roughly comparable with the Hubble radius at the present time. The low-frequency branch of the spectrum can be conventionally defined between νp and νbbn. The largest frequency of the relic graviton spectrum (i.e. νmax is of the order of 0.1 GHz in the ΛCDM scenario. Thus the high-frequency branch of the graviton spectrum can be conventionally defined for νbbn <ν <νmax. In summary we can therefore say that
A schematic view of the frequency range of the relic graviton spectrum (plot at the left) and of the electromagnetic spectrum (plot at the right). In both plots the common logarithms of the (comoving) frequency and of the (comoving) wavelengths are reported, respectively, on the horizontal and on the vertical axis.
• the range νp <ν <νbbn will be generically referred to as the low-frequency domain; in this range the spectrum of relic gravitons basically follows from the minimal ΛCDM paradigm;
• the range νbbn <ν <νmax will be generically referred to as the high-frequency domain; in this range the spectrum of relic gravitons is more uncertain.
The high-frequency branch of the relic graviton spectrum, overlapping with the frequency window of wide-band detectors (see shaded box in the left plot of Fig. 1), is rather sensitive to the thermodynamic history of the plasma after inflation as well as, for instance, to the specific features of the underlying gravity theory at small scales. This is why we said that the theoretical error in the calculation of the relevant observables increases, so to speak, with the frequency.
In Fig. 1 (plot at the right) the electromagnetic spectrum is reported in its salient features. It seems instructive to draw a simple minded parallel between the electromagnetic spectrum and the spectrum of relic gravitons. Consider first the spectrum of relic gravitons (see Fig. 1, plot at the left): between 10-18 Hz (corresponding to νp) and 10 kHz (corresponding to νLV) there are, roughly, 22 decades in frequency. A similar frequency gap (see Fig. 1, plot at the right), if applied to the well known electromagnetic spectrum, would drive us from low-frequency radio waves up to x-rays or γ-rays. As the physics explored by radio waves is very different from the physics probed by γ rays, it can be argued that the informations carried by low and high frequency gravitons originate from two very different physical regimes of the theory. Low frequency gravitons are sensitive to the large scale features of the given cosmological model and of the underlying theory of gravity. High frequency gravitons are sensitive to the small scale features of a given cosmological model and of the underlying theory of gravity.
The interplay between long wavelength gravitons and CMB experiments will be specifically discussed in the subsection 1.2. The main message will be that, according to current CMB experiments, long wavelength gravitons have not been observed yet. The latter occurrence imposes a very important constraint on the low frequency branch of the relic graviton spectrum of the ΛCDM scenario whose salient predictions will be introduced in subsection 1.3. According to the minimal ΛCDM paradigm a very peculiar conclusion seems to pop up: the CMB constraints on the low-frequency tail of the graviton spectrum jeopardize the possibility of any detectable signal for frequencies comparable with the window explored by wide band interferometers (see subsection 1.4). The natural question arising at this point is rather simple: is it possible to have a quasi-flat low-frequency branch of the relic graviton spectrum and a sharply increasing spectral energy density at high-frequencies? This kind of signal is typical of a class of completions of the ΛCDM paradigm which have been recently dubbed TΛCDM (for tensor-ΛCDM). The main predictions of these models will be introduced in subsection 1.5. We shall conclude this introductory section with a discussion of two relevant constraints which should be applied to relic graviton backgrounds in general, i.e. the millisecond pulsar and the big-bang nucleosynthesis constraint (see subsection 1.6).
1.2 Long wavelength gravitons and CMB experiments
The bounds on the backgrounds of relic gravitons stemming from CMB experiments are phrased in terms of rT which is the ratio between the tensor and the scalar power spectra at the same conventional scale (often called pivot scale). While the use of rT is practical (see e. g. the 5-year WMAP data [3–7]), it assumes the ΛCDM scenario insofar as the curvature perturbations are adiabatic. Within the ΛCDM model, the tensor and scalar power spectra can be parametrized as


where kp is the pivot wave-number and  is the amplitude of the power spectrum of curvature perturbations computed at kp; ns and nT are, respectively, the scalar and the tensor spectral indices. The value of kp is conventional and it corresponds to an effective harmonic ℓeff ≃ 30. The perturbations of the spatial curvature, conventionally denoted by ℛ are customarily employed to characterize the scalar fluctuations of the geometry since ℛ is approximately constant (in time) across the radiation-matter transition. As it is clear from Eqs. (1.2) and (1.3) there is a difference in the way the scalar and the tensor spectral indices are assigned: while the scale-invariant limit corresponds to ns → 1 for the curvature perturbations, the scale invariant limit for the long wavelength gravitons corresponds to nT → 0.
is the amplitude of the power spectrum of curvature perturbations computed at kp; ns and nT are, respectively, the scalar and the tensor spectral indices. The value of kp is conventional and it corresponds to an effective harmonic ℓeff ≃ 30. The perturbations of the spatial curvature, conventionally denoted by ℛ are customarily employed to characterize the scalar fluctuations of the geometry since ℛ is approximately constant (in time) across the radiation-matter transition. As it is clear from Eqs. (1.2) and (1.3) there is a difference in the way the scalar and the tensor spectral indices are assigned: while the scale-invariant limit corresponds to ns → 1 for the curvature perturbations, the scale invariant limit for the long wavelength gravitons corresponds to nT → 0.
The figure for  quoted in Eq. (1.3) corresponds to the value inferred from the WMAP 5-year data [3–7] in combination with the minimal ΛCDM model (see also [8–12] for earlier WMAP data releases). In the ΛCDM model the origin of
quoted in Eq. (1.3) corresponds to the value inferred from the WMAP 5-year data [3–7] in combination with the minimal ΛCDM model (see also [8–12] for earlier WMAP data releases). In the ΛCDM model the origin of  stems from adiabatic curvature perturbations which are present after neutrino decoupling but before matter radiation equality (taking place at a redshift
stems from adiabatic curvature perturbations which are present after neutrino decoupling but before matter radiation equality (taking place at a redshift  according to the WMAP 5-yr data [3–5]). The dominant component of curvature perturbations is adiabatic meaning that, over large scales, the fluctuations in the specific entropy are vanishing, at least in the minimal version of the model. The adiabatic nature of the fluctuations induces a simple relation between the first acoustic peak of the TT power spectra and the first anticorrelation peak of the TE power spectra [9]: this is, to date, the best evidence that curvature perturbations are, predominantly, adiabatic. It is useful to translate the comoving wave number kp into a comoving frequency
according to the WMAP 5-yr data [3–5]). The dominant component of curvature perturbations is adiabatic meaning that, over large scales, the fluctuations in the specific entropy are vanishing, at least in the minimal version of the model. The adiabatic nature of the fluctuations induces a simple relation between the first acoustic peak of the TT power spectra and the first anticorrelation peak of the TE power spectra [9]: this is, to date, the best evidence that curvature perturbations are, predominantly, adiabatic. It is useful to translate the comoving wave number kp into a comoving frequency

so, as anticipated, νp is of the order of the aHz. The amplitude at the pivot scale is controlled exactly by rT. In the first release of the WMAP data the scalar and tensor pivot scales were chosen to be different and, in particular, kp = 0.05 Mpc-1 for the scalar modes. In the subsequent releases of data the two pivot scales have been taken to coincide.
The combined analysis of the CMB data, of the large-scale (LSS) structure data [13–16] and of the supernova (SN) data [17–19] can lead to quantitative upper limits on rT which are illustrated in Tabs. 1 and 2 as they are emerge from the combined analyses of different data sets.
The inferred values of the scalar spectral index (i.e. ns), of the dark energy and dark matter fractions (i.e., respectively, ΩΛ and ΩM0), and of the typical wavenumber of equality keq are reported in the remaining columns. While different analyses can be performed, it is clear, by looking at Tabs. 1 and 2, that the typical upper bounds on rT(kp) range between, say, 0.2 and 0.4. More stringent limits can be obtained by adding supplementary assumptions.
In Tab. 1 the quantity αS determines the frequency dependence of the scalar spectral index. In the simplest case αS = 0 and the spectral index is frequency-independent (i.e. ns does not run with the frequency). It can also happen, however, that αS ≠ 0 which implies an effective frequency dependence of the spectral index. If the inflationary phase is driven by a single scalar degree of freedom (as contemplated in the minimal version of the ΛCDM scenario) and if the radiation dominance kicks in almost suddenly after inflation, the whole tensor contribution can be solely parametrized in terms of rT. The rationale for the latter statement is that rT not only determines the tensor amplitude but also, thanks to the algebra obeyed by the slow-roll parameters, the slope of the tensor power spectrum, customarily denoted by nT. To lowest order in the slow-roll expansion, therefore, the tensor spectral index is slightly red and it is related to rT (and to the slow-roll parameter) as

where ϵ measures the rate of decrease of the Hubble parameter during the inflationary epoch. The overdot will denote throughout the paper a derivation with respect to the cosmic time coordinate t while the prime will denote a derivation with respect to the conformal time coordinate τ.
Within the established set of conventions the scalar spectral index ns is given by ns = (1 - 6ϵ + 2 ) and it depends not only upon ϵ but also upon the second slow-roll parameter
) and it depends not only upon ϵ but also upon the second slow-roll parameter  (where V is the inflaton potential, V, φφdenotes the second derivative of the potential with respect to the inflaton field and
(where V is the inflaton potential, V, φφdenotes the second derivative of the potential with respect to the inflaton field and  ). It is sometimes assumed that also nT is not constant but it is rather a function of the wavenumber, i.e.
). It is sometimes assumed that also nT is not constant but it is rather a function of the wavenumber, i.e.

where αT now measures the running of the tensor spectral index.
As already mentioned, among the CMB experiments a central role is played by WMAP [3–7] (see also [8–10] for first year data release and [11, 12] for the third year data release. In connection with [3–7], the WMAP 5-year data have been also combined with observations of the Acbar satellite [20–23] (the Arcminute Cosmology Bolometer Array Receiver (ACBAR) operates in three frequencies, i.e. 150, 219 and 274 GHz). The TT, TE and, partially EE angular power spectra have been measured by the WMAP experiment. Other (i.e. non space-borne) experiments are now measuring polarization observables, in particular there are
-
the Dasi (degree angular scale interferometer) experiment [24–26] operating at south pole;
-
the Capmap (cosmic anisotropy polarization mapper) experiment [27, 28];
-
the BICEP (Background Imaging of Cosmic Extragalactic Polarization) experiment [34, 35];
as well as various other experiments at different stages of development. Other planned experiments have, as specific target, the polarization of the CMB. In particular it is worth quoting here the recent projects Clover [36], Brain [37], Quiet [38], Spider [39] and EBEX [40] just to mention a few. In the near future the Planck explorer satellite [41] might be able to set more direct limits on rT by measuring (hopefully) the BB angular power spectra.
Following the custom the TT correlations will simply denote the angular power spectra of the temperature autocorrelations. The TE and the EE power spectra denote, respectively, the cross power spectrum between temperature and polarization and the polarization autocorrelations.
1.3 The relic graviton spectrum in the ΛCDM model
Having defined the frequency range of the spectrum of relic gravitons, it is now appropriate to illustrate the possible signal which is expected within the ΛCDM scenario.
In Fig. 2 the spectrum of the relic gravitons is reported in the case of the minimal ΛCDM scenario for different values of rT. We remind here that, in the ΛCDM scenario, the dark energy component is always parametrized in terms of a cosmological constant and the spatial curvature of the background geometry vanishes.
The spectral energy density of the relic gravitons is illustrated the context of the ΛCDM scenario and for different values of r T (see Eqs. (1.2)-(1.3)). In the plot at the right the tensor spectral index nT does depend upon the frequency (αT follows from Eq. (1.6) with the ΛCDM choice of parameters). The plot at the left corresponds to αT = 0.
On the horizontal axis the common logarithm of the comoving frequency is reported. The spectral energy density per logarithmic interval of frequency and in critical units is illustrated on the vertical axis. More quantitatively ΩW(ν, τ0) is defined as

where  is the critical energy density. In the present review the ln will denote the natural logarithm while the log will always denote the common logarithm.
is the critical energy density. In the present review the ln will denote the natural logarithm while the log will always denote the common logarithm.
Since ρcrit depends upon  (i.e. the present value of the Hubble rate), it is practical to plot directly
(i.e. the present value of the Hubble rate), it is practical to plot directly  (ν, τ0) at the present (conformal) time τ0. The proper definition of ΩGW(ν, τ0) in terms of the energy-momentum pseudo-tensor in curved space-time is postponed to section 5. The salient features of the relic graviton spectra arising in the context of the ΛCDM scenario can be appreciated by looking carefully at Fig. 2.
(ν, τ0) at the present (conformal) time τ0. The proper definition of ΩGW(ν, τ0) in terms of the energy-momentum pseudo-tensor in curved space-time is postponed to section 5. The salient features of the relic graviton spectra arising in the context of the ΛCDM scenario can be appreciated by looking carefully at Fig. 2.
The infra-red branch of the relic graviton spectrum (see also Fig. 1) extends, approximately, from νp up to a new frequency scale which can be numerically determined by integrating the evolution equations of the tensor modes and of the background geometry across the matter-radiation transition. A semi-analytic estimate of this frequency is given by

At intermediate frequencies Fig. 2 exhibits a further suppression which is due to the coupling of the tensor modes with the anisotropic stress provided by the collisionless species which are present prior to matter-radiation equality. This aspect has been recently emphasized in Ref. [42] (see also [43–45]). Figure 2 assumes that the only colisionless species are provided by massless neutrinos, as the ΛCDM model stipulates and this corresponds, as indicated, to R ν = 0.405. The quantity R ν measures the contribution of N ν families of massless neutrinos to the radiation plasma:

The frequency range of the suppression due to neutrino free-streaming extends from νeq up to νbbn which is given, approximately, by

Both in Eqs. (1.8) and (1.10) ΩM0 and ΩR0 denote, respectively, the present critical fraction of matter and radiation with typical values drawn from the best fit to the WMAP 5-yr data alone and within the ΛCDM paradigm. In Eq. (1.10) g
ρ
denotes the effective number of relativistic degrees of freedom entering the total energy density of the plasma. While νeq is still close to the aHz, νbbn is rather in the nHz range. In Fig. 2 (plot at the left) the spectral index nT is frequency independent; in the plot at the right, always in Fig. 2, the spectral index does depend on the wavenumber. These two possibilities correspond, respectively, to αT = 0 and αT ≠ 0 in Eq. (1.6). In the regime ν <νeq a numerical calculation of the transfer function is mandatory for a correct evaluation of the spectral slope. In the approximation of a sudden transition between the radiation and matter-dominated regimes the spectral energy density goes, approximately, as  . The spectra illustrated have been computed within the approach developed in [46, 47] and include also other two effects which can suppress the amplitude of the quasi-flat plateau, i.e., respectively, the late dominance of the cosmological constant and the progressive reduction in the number of relativistic species. The latter two effects can be estimated analytically (see the final part of section 6) and they are, however, numerically less relevant than neutrino free streaming.
. The spectra illustrated have been computed within the approach developed in [46, 47] and include also other two effects which can suppress the amplitude of the quasi-flat plateau, i.e., respectively, the late dominance of the cosmological constant and the progressive reduction in the number of relativistic species. The latter two effects can be estimated analytically (see the final part of section 6) and they are, however, numerically less relevant than neutrino free streaming.
Apart from the modification induced by the neutrino free-streaming the slope of the spectral energy density for ν > νeq is quasi flat and it is determined by the wavelengths which reentered the Hubble radius during the radiation-dominated stage of expansion. The suggestion that relic gravitons can be produced in isotropic Friedmann-Robertson-Walker models is due to Ref. [48] (see also [49]) and was formulated before the inflationary paradigm. After the formulation of the inflationary scenario the focus has been to compute reliably the low frequency branch of the relic graviton spectrum. In [50–52] the low-frequency branch of the spectrum has been computed with slightly different analytic approaches but always assuming an exact de Sitter stage of expansion prior to the radiation-dominated phase. The analytical calculation (whose details will be described in section 6) shows that in the range νp <ν <νeq, the spectral energy density of the relic gravitons (see Eq. (1.7)) should approximately go as ΩGW(ν, τ0) ≃ ν-2. Within the same approximation, for ν > νeq the spectral energy density is exactly flat (i.e. ΩGW(ν, τ0) ≃ ν0). This result, obtainable by means of analytic calculations (see also [53–56]), is a bit crude in the light of more recent developments. To assess the accurately spectral energy density it is necessary to take into account that the infrared branch is gradually passing from a quasi-flat slope (for ν > νeq) to the slope ν-2 which is the one computed within the sudden approximation [53–56]. It is useful to quote some of the previous reviews which covered, in a more dedicated perspective, the subject of the stochastic backgrounds of relic gravitons. The review article by Thorne [57] does not deal solely with relic graviton backgrounds while the reviews of Refs. [58–60] are more topical.
The flat plateau of the spectral energy density extends, approximately, between νeq and a certain νmax. Also the maximal amplified frequency can be computed once the model of smooth transition between inflation and radiation is known. The smoothness of the transition determines specifically the precise amount of exponential suppression for ν > νmax. A simple estimate of νmax is given by

where, as in Eqs. (1.2) and (1.3),  denotes the amplitude of the power spectrum of curvature perturbations evaluated at the pivot wavenumber νp. It is worth noticing that between νbbn and νmax there are approximately 20 orders of magnitude in frequency. In the ΛCDM scenario the spectrum has, in this range, always the same slope (i.e. nT is frequency-independent in Eq. (1.2)).
denotes the amplitude of the power spectrum of curvature perturbations evaluated at the pivot wavenumber νp. It is worth noticing that between νbbn and νmax there are approximately 20 orders of magnitude in frequency. In the ΛCDM scenario the spectrum has, in this range, always the same slope (i.e. nT is frequency-independent in Eq. (1.2)).
Some details of the calculations leading to the spectral energy densities illustrated in Fig. 2 can be found in sections 5 and 6. Without dwelling on the details it is however clear, as anticipated, that the constraints on the long wavelength gravitons make it difficult (if not impossible) to have a detectable spectral energy density at the scale of wide-band interferometers. The latter statement, valid in the minimal ΛCDM scenario, will be sharpened in the following subsection.
1.4 Short wavelength gravitons and wide-band interferometers
In the ΛCDM scenario the spectral energy density of the relic gravitons has its larger amplitude in the low-frequency branch. As the frequency increases the spectral energy density diminishes so that it is plausible to expect a rather small amplitude over the frequencies corresponding to wide-band interferometers (see, for instance, Fig. 2 for ν ≃ νLV = 100 Hz).
Wide-band interferometers operate in a window ranging from few Hz up to 10 kHz (see also Fig. 1). The available interferometers are Ligo [61], Virgo [62], Tama [63] and Geo [64]. In loose terms these instruments are Michelson interferometers with two important differences: the mirrors are suspended and Fabry-Pérot cavities are used to increase the optical path of the photons. It would be too pretentious to describe in detail, in the present script, also the experimental apparatus and we therefore suggest Ref. [65] where the basics of wide-band interferometers are introduced in a self-contined perspective.
The sensitivity of a given pair of wide-band detectors to a stochastic background of relic gravitons depends upon the relative orientation of the instruments. The wideness of the band (important for the correlation among different instruments) is not as large as 10 kHz but typically narrower and, in an optimistic perspective, it could range up to 100 Hz. The putative frequency of wide-band detectors will therefore be indicated as νLV, i.e. in loose terms, the Ligo/Virgo frequency. There are daring projects of wide-band detectors in space like the Lisa [66], the Bbo [67] and the Decigo [68] projects. The common feature of these three projects is that they are all space-borne missions and that they are all sensitive to frequencies smaller than the mHz (1 mHz = 10-3 Hz). While wide-band interferometers are now operating and might even reach their advanced sensitivities during the incoming decade, the wished sensitivities of space-borne interferometers are still on the edge of the achievable technologies.
Since νbbn <νLV <νmax, wide-band interferometers represent an ideal instrument to investigate the relic graviton spectrum at high-frequencies. The spectral energy density of the relic gravitons produced within the ΛCDM model is quite minute and it is undetectable by interferometers even in their advanced version where the sensitivity is expected to improve by 5 or even 6 orders of magnitude in comparison with the present performances [69–71] (see also [72] and [73]). In Fig. 3 the spectral energy density is reported for ν = νLV and always in the case of the prediction stemming from the minimal ΛCDM scenario.
The spectral energy density of the relic gravitons in the context of the ΛCDM model evaluated at the Ligo/Virgo frequency as a function of the tensor-to-scalar ratio. In the plot at the right the spectral index does not run (see Eq. (1.5)) while in the left plot the spectral index does run and it is given by Eq. (1.6). To guide the intuition consider that (advanced) wide-band interferometers will achieve, optimistically, a sensitivity of 10-10 in ΩGW(ν, τ0). Taking into account the current bounds on rT (see Tabs. 1 and 2) it is clear that the ΛCDM scenario is definitively too small to provide a serious target for wide-band detectors.
In Fig. 3, the common logarithm of the spectral energy density is illustrated as a function of the common logarithm of rT.
In Ref. [70] (see also [69, 71]) the current limits on the presence of an isotropic background of relic gravitons have been assessed. According to the Ligo collaboration (see Eq. (19) of Ref. [70]) the spectral energy density of a putative (isotropic) background of relic gravitons can be parametrized as:

The variable β is used in Eq. (1.12) just because this is the notation endorsed by the Ligo collaboration and there is no reason to change it. At the same time, in the present review, β will be used also with different meanings. In section 6, β quantifies the theoretical error on the maximal frequency of the relic graviton spectrum(see e.g. Eq. (6.48) and discussion therein). In section 7, β parametrizes a portion of the azimuthal structure of the Stokes parameters. Since none of these variables appear in the same context, potential clashes of conventions are avoided.
The parametrization of Eq. (1.12) fits very well with Fig. 3 where the pivot frequency νLV = 100 Hz coincides with the pivot frequency appearing in the parametrization (1.12). For the scale-invariant case (i.e. β = -3 in eq. (1.12)) the Ligo collaboration sets a 90% upper limit of 1.20 × 10-4 on the amplitude appearing in Eq. (1.12), i.e. ΩGW,-3. Using different sets of data (see [69, 71]) the Ligo collaboration manages to improve the bound even by a factor 2 getting down to 6.5 × 10-5. Thus Fig. 3 together with the upper limit of Eq. (1.12) shows that the current Ligo sensitivity is still too small to detect the relic graviton background arising within the ΛCDM paradigm.
1.5 Beyond the ΛCDM paradigm and high-frequency gravitons
In the case of an exactly scale invariant spectrum the correlation of the two (coaligned) LIGO detectors with central corner stations in Livingston (Lousiana) and in Hanford (Washington) might reach a sensitivity to a at spectrum which is [74–76]

where T denotes the observation time and SNR is the signal to noise ratio. Equation (1.13) is in close agreement with the sensitivity of the advanced Ligo apparatus [61] to an exactly scale-invariant spectral energy density [77–81]. Equation (1.13) together with the plots of Fig. 3 suggest that the relic graviton background predicted by the ΛCDM paradigm is not directly observable by wide-band interferometers in their advanced version.
CMB observations probe the aHz region of the spectral energy density of Fig. 2. Wide-band interferometers probe a frequency range between few Hz and 10 kHz. In both ranges, the signal of the ΛCDM scenario might be too small to be directly detectable.
In Fig. 4 the spectral energy density is computed in an extension of the ΛCDM paradigm which has been dubbed tensor-ΛCDM (TΛCDM for short) [46, 47]. In the TΛCDM scenario the transition from the inflationary phase to the radiation-dominated epoch is mediated by a rather long stiff phase. By stiff phase we mean a phase where the total sound speed of the plasma is larger than the sound speed of a radiation-dominated plasma (i.e. 1/ in natural units). In the simplest realization of the scenario the barotropic index wt is constant during the stiff phase. For instance, in Fig. 4 the cases wt = 1 and wt = 0.6 have been illustrated. Since wt denotes the ratio between the total pressure and the total energy density, it is rather plausible to demand that wt ≤ 1. The latter requirement implies that the sound speed is always smaller than the speed of light. As suggested in [82] (see also [83, 84]) the presence of a stiff phase can have the effect of increasing the spectral energy density at high frequencies. The increase takes place for frequencies larger than the mHz and is typically maximal in the GHz region. The spectral energy densities illustrated in Fig. 4 suggest that it is not impossible to imagine situations where the spectral energy density of the relic gravitons satisfies all the constraints demanded by CMB physics but, at the same time, it is sufficiently large to be observed by wide-band interferometers. The results reported in Fig. 4 refer to the minimal TΛCDM model where only one post-inflationary phase stiffer than radiation is contemplated. The barotropic index could have, however, a more complicated dependence. Already in the examples of Fig. 4 the numerical integration implies that the barotropic index does depend, effectively, upon the scale factor (see, e. g., discussions in section 6 on the transfer function for the spectral energy density).
in natural units). In the simplest realization of the scenario the barotropic index wt is constant during the stiff phase. For instance, in Fig. 4 the cases wt = 1 and wt = 0.6 have been illustrated. Since wt denotes the ratio between the total pressure and the total energy density, it is rather plausible to demand that wt ≤ 1. The latter requirement implies that the sound speed is always smaller than the speed of light. As suggested in [82] (see also [83, 84]) the presence of a stiff phase can have the effect of increasing the spectral energy density at high frequencies. The increase takes place for frequencies larger than the mHz and is typically maximal in the GHz region. The spectral energy densities illustrated in Fig. 4 suggest that it is not impossible to imagine situations where the spectral energy density of the relic gravitons satisfies all the constraints demanded by CMB physics but, at the same time, it is sufficiently large to be observed by wide-band interferometers. The results reported in Fig. 4 refer to the minimal TΛCDM model where only one post-inflationary phase stiffer than radiation is contemplated. The barotropic index could have, however, a more complicated dependence. Already in the examples of Fig. 4 the numerical integration implies that the barotropic index does depend, effectively, upon the scale factor (see, e. g., discussions in section 6 on the transfer function for the spectral energy density).
The spectral energy density of relic gravitons in the minimal TΛCDM scenario where the post-inflationary thermal history contemplates a phase where the sound speed of the plasma c st is close to the speed of light c. In the plot at the right cst = c (corresponding to a constant barotropic index wt = 1); in the plot at the left cst = 0.77 c (corresponding to a constant barotropic index wt = 0.6). In both plots the other cosmological parameters have been chosen to coincide with the best fit to the WMAP 5-yr data alone.
The comparison of Fig. 2 and 4 suggests, in short, the following subjects of reflection:
-
the theoretical error in the estimate of the spectral energy density increases with the frequency;
-
departures from the standard post-inflationary thermal history can be directly imprinted in the primordial spectrum of the relic gravitons;
-
in the incoming decade the observations of wide-band interferometers could be analyzed in conjunction with more standard data sets (i.e. CMB data supplemented by large-scale structure data and by the observations of type Ia supernovae) to constrain the spectral energy density of the relic gravitons both at small and at high frequencies.
The presence of post-inflationary phases stiffer than radiation is, after all, rather natural and this was the original spirit of [82]. We do not know which was the rate of the post-inflationary expansion and since guesses cannot substitute experiments it would be productive to use the TΛCDM paradigm as reference model for a unified analysis of the low-frequency data stemming from CMB and of the high-frequency data provided by wide-band interferometers. Already in [82] (see also [83, 84]) a rather special candidate for a post-inflationary phase stiffer than radiation was the case when the sound speed equals the speed of light, i.e. the case when the energy density of the sources driving the geometry is dominated by the kinetic term of a (minimally coupled) scalar field. This particular case was also prompted by various classes of quintessence models. A specific example of this dynamics was provided in [85].
A more detailed account of the techniques leading to Fig. 4 will be swiftly presented in section 6 and can be found in [46, 47]. Without going through the details it is however important to stress that the calculations should be accurate enough not only in the high-frequency region but also in the low-frequency part of the spectrum. Indeed, as stressed above, one of the purposes of the TΛCDM scenario is to convey the idea that low-frequency and high-frequency measurements of the relic graviton background can be analyzed in a single theoretical framework.
1.6 The millisecond pulsar bound and the nucleosynthesis constraint
The spectral energy density of the relic gravitons must be compatible not only with the CMB constraints (bounding, from above, the value of rT) but also with the pulsar timing bound[86, 87] and the big-bang nucleosynthesis constraints [88–90]. The pulsar timing bound demands

where νpulsar roughly corresponds to the inverse of the observation time during which the pulsars timing has been monitored. The spectral energy densities illustrated in Figs. 2 and 4 satisfy the pulsar timing bound.
The most constraining bound for the high-frequency branch of the relic graviton spectrum is represented by big-bang nucleosynthesis. Gravitons, being relativistic, can potentially increase the expansion rate at the BBN epoch. The increase in the expansion rate will affect, in particular, the synthesis of 4He. To avoid the overproduction of 4He the expansion rate the number of relativistic species must be bounded from above.
The BBN bound is customarily expressed in terms of (equivalent) extra fermionic species. During the radiation-dominated era, the energy density of the plasma can be written as ρt = g ρ (π2/30)T4 where T denotes here the common (thermodynamic) temperature of the various species. An (ultra)relativistic fermion species with two internal degrees of freedom and in thermal equilibrium contributes 2·7/8 = 7/4 = 1.75 to g ρ . Before neutrino decoupling the contributing relativistic particles are photons, electrons, positrons, and N ν = 3 species of neutrinos, giving

The neutrinos have decoupled before electron-positron annihilation so that they do not contribute to the entropy released in the annihilation. While they are relativistic, the neutrinos still retain an equilibrium energy distribution, but after the annihilation their (kinetic) temperature is lower, T ν = (4/11)1/3T. Thus

after electron-positron annihilation. By now assuming that there are some additional relativistic degrees of freedom, which also have decoupled by the time of electron-positron annihilation, or just some additional component ρX to the energy density with a radiation-like equation of state (i.e. pX = ρX/3), the effect on the expansion rate will be the same as that of having some (perhaps a fractional number of) additional neutrino species. Thus its contribution can be represented by replacing N
ν
with N
ν
+ ΔN
ν
in the above. Before electron-positron annihilation we have ρX = (7/8)ΔN
ν
ρ
γ
and after electron-positron annihilation we have ρX = (7/8)(4/11)4/3 ΔN
ν
ρ
γ
≃ 0.227 ΔN
ν
ρ
γ
. The critical fraction of CMB photons can be directly computed from the value of the CMB temperature and it is notoriously given by  ≡ ργ/ρcrit = 2.47 × 10-5. If the extra energy density component has stayed radiation-like until today, its ratio to the critical density, ΩX, is given by
≡ ργ/ρcrit = 2.47 × 10-5. If the extra energy density component has stayed radiation-like until today, its ratio to the critical density, ΩX, is given by

If the additional species are relic gravitons, then [88–90]:

where νbbn and νmax are given, respectively, by Eqs. (6.61) and (8.4). Thus the constraint of Eq. (1.18) arises from the simple consideration that new massless particles could eventually increase the expansion rate at the epoch of BBN. The extra-relativistic species do not have to be, however, fermionic [89] and therefore the bounds on ΔN ν can be translated into bounds on the energy density of the relic gravitons.
A review of the constraints on ΔN ν can be found in [89]. Depending on the combined data sets (i.e. various light elements abundances and different combinations of CMB observations), the standard BBN scenario implies that the bounds on ΔN ν range from ΔN ν ≤ 0.2 to ΔN ν ≤ 1. Similar figures, depending on the priors of the analysis, have been obtained in a more recent analysis [90]. All the relativistic species present inside the Hubble radius at the BBN contribute to the potential increase in the expansion rate and this explains why the integral in Eq. (1.18) must be performed from νbbn to νmax (see also [83] where this point was stressed in the framework of a specific model). The existence of the exponential suppression for ν > νmax (see Figs. 4) guarantees the convergence of the integral also in the case when the integration is performed up to ν → ∞. The constraint of Eq. (1.18) can be relaxed in some non-standard nucleosynthesis scenarios [89], but, in what follows, the validity of Eq. (1.18) will be enforced by adopting ΔN ν ≃ 1 which implies, effectively

The spectral energy densities illustrated in Figs. 2 and 4 are both compatible with the big-bang nucleosynthesis bound. Thus the big-bang nucleosyntheis constraint does not forbid a potentially detectable signal in the high-frequency branch of the relic graviton spectrum. Potential deviations of the thermal history of the plasma must anyway occur before big-bang nucleosynthesis.
2 The polarization of relic gravitons and of relic photons
2.1 Basic notations
As discussed in the introduction, in the ΛCDM paradigm the background line element can be written

where, in the spatially flat case,  will coincide with δ
ij
and the Friedmann-Lemaître equations can be written as
will coincide with δ
ij
and the Friedmann-Lemaître equations can be written as



where ℋ = a'/a; the prime denotes a derivation with respect to the conformal time coordinate τ. The Hubble rate is customarily defined in the synchronous frame where the time coordinate (conventionally denoted by t) obeys dt = a(τ)dτ. Denoting with a dot a derivation with respect to the cosmic time t, H =  /a, and, by definition, H = aℋ. In Eqs. (2.2)-(2.4) ρt and pt are, respectively, the total energy density and the total pressure of the plasma, i.e.
/a, and, by definition, H = aℋ. In Eqs. (2.2)-(2.4) ρt and pt are, respectively, the total energy density and the total pressure of the plasma, i.e.


The total matter fraction of the critical energy density, i.e. ΩM0 = ρM0/ρcrit consists of baryons and (i.e. ρb) and cold dark matter particles (i.e. ρc). In Tabs. 1 and 2 the values of ΩM0 are given as they are inferred within the ΛCDM scenario. In similar terms ΩΛ = ρΛ/ρcrit denotes the critical fraction of dark energy. In what follows, if not otherwise stated, the cosmological parameters will be fixed to the best fit of the WMAP-5 yr data alone, i.e.

where Ωb0, Ωc0, ΩΛ denote, respectively, the (present) critical fractions of baryons, CDM particles and dark energy; h0 fixes the present value of the Hubble rate; ns, as already mentioned in section 1, is the spectral index of curvature perturbations and ϵ is the reionization optical depth.
At the beginning of the previous section we started by stressing analogies and differences between relic gravitons and relic photons. The most important one is that both gravitons and photons carry two polarizations. This observation is important for a quantitative understanding of the present endevours aimed at measuring the E-mode and the B-mode polarization of the CMB. In the present section the description of the polarization of the gravitons will be developed by stressing, when possible, the analogy with polarization observables of the electromagnetic field.
2.2 Linear and circular tensor polarizations
Recalling that i, j, k, ... are indices defined on the three-dimensional Euclidean sub-manifold, the tensor fluctuations of the geometry are parametrized in terms of the rank-two tensor h ij

where ∇
i
is the covariant derivative with respect to  ; if
; if  = δ
ij
, ∇
i
= ∂
i
. In Eq. (2.8) the subscript refers to the tensor nature of the fluctuation while the superscript denotes the perturbative order. The tensor fluctuation h
ij
(
= δ
ij
, ∇
i
= ∂
i
. In Eq. (2.8) the subscript refers to the tensor nature of the fluctuation while the superscript denotes the perturbative order. The tensor fluctuation h
ij
( , τ) can be decomposed in terms of the two linear polarizations, i.e.
, τ) can be decomposed in terms of the two linear polarizations, i.e.

where λ = ⊕, ⊗ denote the two polarizations and where


In Eqs. (2.10) and (2.11),  ,
,  and
and  represent a triplet of mutually orthogonal unit vectors, i.e.
represent a triplet of mutually orthogonal unit vectors, i.e.

If the direction of propagation coincides with the  , the unit vectors
, the unit vectors  ,
,  and
and  can be chosen as:
can be chosen as:

Using Eq. (2.13), Eqs. (2.10) and (2.11) become


If  coincides with the radial direction, the unit vectors
coincides with the radial direction, the unit vectors  ,
,  and
and  can be chosen, in spherical coordinates, as:
can be chosen, in spherical coordinates, as:



Since  , it is straightforward to prove that
, it is straightforward to prove that

As in the case of electromagnetic waves, it is often desirable to pass from the linear to the circular polarizations:


Equations (2.20) and (2.21) also imply that  and
and  . A rotation of
. A rotation of  and
and  in the plane orthogonal to
in the plane orthogonal to 


implies, using Eqs. (2.10) and (2.11),


where the tilde denotes the two transformed (linear) polarizations. Under the transformation given in Eqs. (2.22) and (2.23) the two circular polarizations defined in Eqs. (2.20) and (2.21) transform as

The transformation properties of the circular polarization under a rotation in the plane orthogonal to the direction of propagation are closely analog to the transformation properties, under the same rotation, of the polarization of the electromagnetic field. This analogy will now be exploited to introduce the E-mode and B-mode polarization.
Before proceeding with the discussion it is appropriate to recall a very basic aspect of rotations which can have, however, some confusing impact of the polarization analysis especially in the case of the tensor modes. Consider, for simplicity, a coordinate system characterized by two basis vectors, i.e.  cos ϑ and
cos ϑ and  sin ϑ. If we now perform a clockwise (i.e. right-handed) rotation of the axes
sin ϑ. If we now perform a clockwise (i.e. right-handed) rotation of the axes  and
and  , the rotated basis
, the rotated basis  will be given as in Eqs. (2.22) and (2.23) by replacing
will be given as in Eqs. (2.22) and (2.23) by replacing  and
and  . Some authors, for different reasons, instead of rotating the coordinate system prefer to rotate the polarization vector. If angles are in the right-handed sense for the rotation of the axes, they are in the left-handed sense for the rotation of the vectors.
. Some authors, for different reasons, instead of rotating the coordinate system prefer to rotate the polarization vector. If angles are in the right-handed sense for the rotation of the axes, they are in the left-handed sense for the rotation of the vectors.
2.3 Polarization of the CMB radiation field
The radiation field can be described by the polarization tensor, i.e.

where E
i
and E
j
are the electric components of the radiation field. Assuming, for sake of simplicity, that the radiation field propagate along the  axis, then the various entries of ρ
ij
can be written in a matrix form
axis, then the various entries of ρ
ij
can be written in a matrix form

where x and y denote the components of the electric field orthogonal to the direction of propagation coinciding, in this set-up, with the third Cartesian axis. A full description of the radiation field can be achieved by studying the four Stokes parameters [91] conventionally named I, Q, U and V:


It is immediate, from the definitions (2.29) and (2.30), to write the intensities of the radiation field along the different Cartesian axis as a function of the Stokes parameters, i.e.


Equations (2.31) and (2.32) can be inserted back into Eq. (2.28) with the result that

where

From Eq. (2.33) it also follows that

where 1 is the 2 × 2 unit matrix and

are the Pauli matrices. Consider now a rotation of an angle α on the plane orthogonal to the direction of propagation of the monochromatic wave. It is easy to show that I and V are left invariant while Q and U do transform by a rotation of 2α. By indicating with a tilde the transformed Stokes parameters the result can be expressed as

Equations (2.24)-(2.25) and (2.37) express the fact that the polarization of the graviton and of the radiation field do change for a rotation on the plane orthogonal to the direction of propagation of the radiation (either gravitational or electromagnetic). It is possible to construct polarization observables which are invariant for rotations on the plane orthogonal to the direction of propagation of the radiation: because of their properties under parity transformations they are called E-and B-modes.
2.4 E- and B-modes
The fluctuations of the geometry induce fluctuations of the Stokes parameters whose spectral properties are, ultimately, the aim of CMB polarization experiments. In general terms the fluctuation of each Stokes parameter can be written as



In Eqs. (2.38)-(2.40) the superscript reminds that the various fluctuations of the Stokes parameters are induced, respectively, by the tensor, scalar and vector modes of the geometry. While some of the results of the present section will be generally valid, the focus, in what follows, will be on the tensor contribution. Defining the two linear combinations

and denoting with a tilde the transformed quantities, Eq. (2.37) implies that Δ± ( , τ) transform as
, τ) transform as

In more general terms, consider a generic function of  (be it f(
(be it f( )). Under a rotation of an angle α on the plane orthogonal to
)). Under a rotation of an angle α on the plane orthogonal to  , f(
, f( ) is said to transform as a function of (integral) spin-weight ± s provided
) is said to transform as a function of (integral) spin-weight ± s provided

In other words Δ+( ) and Δ-(
) and Δ-( ) transform, respectively, as functions of spin weight +2 and -2. The circular polarizations of the gravitons introduced in Eqs. (2.24)-(2.25) transform, respectively, as functions of spin weight +2 and -2. The brightness perturbations for the intensity of the radiation field (i.e. ΔI(
) transform, respectively, as functions of spin weight +2 and -2. The circular polarizations of the gravitons introduced in Eqs. (2.24)-(2.25) transform, respectively, as functions of spin weight +2 and -2. The brightness perturbations for the intensity of the radiation field (i.e. ΔI( )) transform, on the contrary, as quantities of spin weight 0. The fluctuations in the intensity of the radiation field, being a spin-0 quantity, can be expanded in ordinary spherical harmonics as
)) transform, on the contrary, as quantities of spin weight 0. The fluctuations in the intensity of the radiation field, being a spin-0 quantity, can be expanded in ordinary spherical harmonics as

The spin-s quantity will naturally be expanded in terms of a generalization of the ordinary spherical harmonics which are called spin-s spherical harmonics or also spin-weighted spherical harmonics. Owing to this observation, Δ±( , τ) can be expanded in terms of spin-±2 spherical harmonics ±2Yℓm(
, τ) can be expanded in terms of spin-±2 spherical harmonics ±2Yℓm( ), i.e.
), i.e.

Given a quantity of spin-weight s it is possible to construct quantities of spin-weight 0 by the repeated use of appropriate differential operators which can either raise or lower the spin-weight of a given function (see subsection 2.5 for a specific discussion). Consequently, from Δ+( , τ) and Δ-(
, τ) and Δ-( , τ) it is possible to construct two fluctuations of spin 0 which can be eventually expanded in ordinary spherical harmonics. By demanding that the two fluctuations of spin-weight 0 are eigenstates of parity the E- and B-modes are defined as
, τ) it is possible to construct two fluctuations of spin 0 which can be eventually expanded in ordinary spherical harmonics. By demanding that the two fluctuations of spin-weight 0 are eigenstates of parity the E- and B-modes are defined as

where

From  ,
, 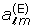 and
and  the angular power spectra can be defined. In particular the EE, BB, TT and TE angular power spectra are given by:
the angular power spectra can be defined. In particular the EE, BB, TT and TE angular power spectra are given by:


where ⟨...⟩ denotes the ensemble average. Two further power spectra can be defined and they are:

Overall, the existence of linear polarization allows for 6 different power spectra.
In the minimal version of the ΛCDM paradigm the adiabatic fluctuations of the scalar curvature lead to a polarization which is characterized exactly by the condition a2, ℓm= a-2, ℓm, i.e.  = 0. This observation implies that, in the ΛCDM scenario, the non-vanishing angular power spectra are given by the TT, EE and TE correlations. In the TΛCDM scenario the TT, EE and TE angular power spectra are supplemented by a specific prediction for the B-mode autocorrelation (see section 7).
= 0. This observation implies that, in the ΛCDM scenario, the non-vanishing angular power spectra are given by the TT, EE and TE correlations. In the TΛCDM scenario the TT, EE and TE angular power spectra are supplemented by a specific prediction for the B-mode autocorrelation (see section 7).
2.5 Spin-2 spherical harmonics
Spherical harmonics of higher spin appear in matrix elements calculations in nuclear physics (see e.g. the classic treatise of Blatt and Weisskopf [92], and, in a similar perspective the book of Edmonds [93]). The comprehensive treatments of Biedenharn and Louk [94] and of Varshalovich et al. [95] can also be usefully consulted.
The spin-s harmonics have been introduced, in their present form, by Newman and Penrose [96] and their group theoretical interpretation has been discussed in [97]. The spin-s spherical harmonics have been applied to the discussion of CMB polarization induced by relic gravitons in a number of papers [98–100]. They are rather crucial in the formulation of the so-called total angular momentum approach. Discussions of the spin-weighted spherical harmonics in a cosmological context can also be found in [101, 102]. The spin weighted spherical harmonics will now be introduced by following the spirit of Ref. [97] which has been also used, with different conventions, in [98]. In subsection 2.6 the (equivalent) approach of [99, 100] will be more specifically outlined.
Th functions ±2Yℓm( ) appearing in Eq. (2.45) are the spin-2 spherical harmonics [97]. Consider the representations of the operator specifying three-dimensional rotations, i.e.
) appearing in Eq. (2.45) are the spin-2 spherical harmonics [97]. Consider the representations of the operator specifying three-dimensional rotations, i.e.  ; this problem is usually approached within the matrix element, i.e.
; this problem is usually approached within the matrix element, i.e.  where j denotes the eigenvalue of J2 and m denotes the eigenvalue of Jz. Now, if we replace m' → -s, j → ℓ, we have the definition of spin-s spherical harmonics in terms of the
where j denotes the eigenvalue of J2 and m denotes the eigenvalue of Jz. Now, if we replace m' → -s, j → ℓ, we have the definition of spin-s spherical harmonics in terms of the  , i.e.
, i.e.

where α, β and γ (set to zero in the above definition) are the Euler angles defined as in [103]. If s = 0,  where Yℓm(α, β) are the ordinary spherical harmonics. The spin-s spherical harmonics can be obtained from the spin-0 spherical harmonics by using repeatedly the differential operators:
where Yℓm(α, β) are the ordinary spherical harmonics. The spin-s spherical harmonics can be obtained from the spin-0 spherical harmonics by using repeatedly the differential operators:


The notation spelled out in Eqs. (2.52) and (2.53) (which is not usual) will be employed to emphasize the interpretation of  as ladder operators (see [97]). The operator
as ladder operators (see [97]). The operator  raises the spin weight of a function by one unit. Consider, therefore, the ordinary spherical harmonics Yℓm(
raises the spin weight of a function by one unit. Consider, therefore, the ordinary spherical harmonics Yℓm( ) defined as
) defined as


where Pℓ(μ) are the Legendre polynomials and  (μ) the associated Legendre functions. It is appropriate to mention here that the factor (-1)m(i.e. Condon-Shortley phase) can either be included in the normalization factor
(μ) the associated Legendre functions. It is appropriate to mention here that the factor (-1)m(i.e. Condon-Shortley phase) can either be included in the normalization factor  or (as it has been done) in the definition of the associated Legendre functions appearing in Eq. (2.55). When using the recurrence relations of the associated Legendre functions the Condon-Shortley phase introduces a sign difference every time m is odd. The conventions expressed by Eqs. (2.54) and (2.55) will be followed throughout the present discussion and, in particular, in section 7 where the correlation functions of the E-modes and of the B-modes will be specifically computed with different techniques.
or (as it has been done) in the definition of the associated Legendre functions appearing in Eq. (2.55). When using the recurrence relations of the associated Legendre functions the Condon-Shortley phase introduces a sign difference every time m is odd. The conventions expressed by Eqs. (2.54) and (2.55) will be followed throughout the present discussion and, in particular, in section 7 where the correlation functions of the E-modes and of the B-modes will be specifically computed with different techniques.
According to Eq. (2.43), Yℓmtransform with s = 0, i.e. they have spin weight 0. By applying once  to Yℓm(
to Yℓm( ) we do get a function of spin weight 1, i.e.
) we do get a function of spin weight 1, i.e.

We can then apply once more  to
to  and the result of this simple manipulation will be
and the result of this simple manipulation will be

This time, in  , s = 1 since
, s = 1 since  is a quantity of spin weight 1.
is a quantity of spin weight 1.
The right hand side of Eq. (2.57) is +2Yℓm(ϑ, φ) (up to an overall normalization). Including the appropriate normalization factor, ±2Yℓm(ϑ, φ), i.e. the spherical harmonics of spin weight s = ± 2 are given by:

The spin weights s = ± 2 are both needed since the transformation of the polarization involve both spin weights (see Eq. (2.45)). In fact, since ±2Yℓm(ϑ, φ) form a complete and orthogonal basis on the sphere, i.e.


Δ± ( , τ) can be expanded in terms of ±2Yℓm(ϑ, φ) as in Eq. (2.45). The coefficients off the expansion will be given by
, τ) can be expanded in terms of ±2Yℓm(ϑ, φ) as in Eq. (2.45). The coefficients off the expansion will be given by


Integrating by parts in Eqs. (2.61) and (2.62) allows for a different form of the expansion coefficients a±2, ℓm:


where, as already mentioned,  . In Eqs. (2.63) and (2.64) there appear only ordinary (i.e. spin-weight 0) spherical harmonics. This occurrence suggests a complementary approach to the problem: instead of expanding Δ± (
. In Eqs. (2.63) and (2.64) there appear only ordinary (i.e. spin-weight 0) spherical harmonics. This occurrence suggests a complementary approach to the problem: instead of expanding Δ± ( , τ) in terms of spin-2 spherical harmonics, fluctuations of spin-weight 0 can be directly constructed (in real space) from Δ± (
, τ) in terms of spin-2 spherical harmonics, fluctuations of spin-weight 0 can be directly constructed (in real space) from Δ± ( , τ) by repeated application of the ladder operators defined in Eqs. (2.52) and (2.53).
, τ) by repeated application of the ladder operators defined in Eqs. (2.52) and (2.53).
The E-mode and B-mode polarization in real space are then, in explicit terms:


The quantities ΔE( , τ) and ΔB(
, τ) and ΔB( , τ) can be expanded in terms of ordinary spherical harmonics, as already suggested in Eq. (2.46):
, τ) can be expanded in terms of ordinary spherical harmonics, as already suggested in Eq. (2.46):

The "electric" and "magnetic" components of polarization are eigenstates of parity and may be defined, from a±, ℓmas already mentioned in Eq. (2.47):

Under parity the components appearing in Eqs. (2.68) transform

Therefore, the E-modes have the same parity of the temperature correlations which have, in turn, the same parity of conventional spherical harmonics, i.e. (-1)ℓ. On the contrary, the B-modes have (-1)ℓ+1parity. The same analysis can be directly performed in real space, i.e. using Eqs. (2.65) and (2.66). Denoting the radial direction with  and the tangential directions with
and the tangential directions with  and
and  , the ladder operators defined in Eqs. (2.52) and (2.53) are consistent with the following choice of
, the ladder operators defined in Eqs. (2.52) and (2.53) are consistent with the following choice of  and
and  :
:

As discussed at the end of subsection 2.1 the sign of φ can be flipped. This possibility is not related to a parity transformation and it has to do with the way two-dimensional rotations are introduced. This aspect will also be relevant in section 7 for explicit derivations.
A parity transformation (i.e. a space inversion) implies, in spherical coordinates, that

The transformation (2.71) implies that the two basis vectors defined in Eq. (2.70) transform as  and
and  , i.e. while
, i.e. while  does not change
does not change  flips its sign under space inversion. It follows that space-inversion does not flip the sign of ΔE(
flips its sign under space inversion. It follows that space-inversion does not flip the sign of ΔE( ) but it does flip the sign of ΔB(
) but it does flip the sign of ΔB( ), i.e. under the transformation (2.71), ΔE(
), i.e. under the transformation (2.71), ΔE( ) → ΔE(
) → ΔE( ) while ΔB(
) while ΔB( ) → -ΔB(
) → -ΔB( ).
).
Using Eqs. (2.63) and (2.64) inside Eq. (2.68) a more explicit expression for 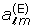 and
and  can be obtained and it is:
can be obtained and it is:


The contribution of long wavelength gravitons to Eqs. (2.72) and (2.73) will be discussed in section 7. It is often useful to observe that the differential operators appearing in the definition of the spin-weighted spherical harmonics (see, e.g. Eq. (2.58)) can be expressed in terms of the usual differential operators arising in the theory of the orbital angular momentum in non-relativistic quantum mechanics (see, e. g. [103]). Indeed, recalling that


it can be easily deduced that



Equations (2.76)-(2.78) allow often to express combinations of spin-2 spherical harmonics in terms of ordinary (i.e. spin-weight 0) spherical harmonics using the properties of the ladder operators associated to the (orbital) angular momentum, i.e. L±:

where L± and Lz obey the well known commutation relations [L±, L z ] = ∓L± and [L+, L-] = 2L z .
Looking at Eq. (2.79) it is tempting draw a parallel between the (orbital) ladder operators and the ladder operators raising (or lowering) the spin weight of a given function (see Eqs. (2.52) and (2.53). This problem has been discussed and solved in [97]. It is possible to formulate the parallel in terms of a putative O(4) group. Half of the generators will be connected with the orbital angular momentum operators, while the other half will allow to increase (or decrease) the spin weight of a given function. The two sets of generators commute. The operators  are not directly, though, the ladder operators stemming from the second set of generators. This has to do with the fact that in Eq. (2.51) the third Euler angle (i.e. γ) has been fixed to zero. The
are not directly, though, the ladder operators stemming from the second set of generators. This has to do with the fact that in Eq. (2.51) the third Euler angle (i.e. γ) has been fixed to zero. The  are ladder operators defined within a putative O(4) group in the case γ ≠ 0. When γ → 0 the dependence upon γ drops and we are left with Eqs. (2.52) and (2.53).
are ladder operators defined within a putative O(4) group in the case γ ≠ 0. When γ → 0 the dependence upon γ drops and we are left with Eqs. (2.52) and (2.53).
2.6 Polarization on the 2-sphere
In a more geometric perspective, the spin-2 harmonics are introduced by describing the polarization tensor on the 2-sphere which represents the microwave sky. In Eq. (2.34) the tensor P
ij
describes the properties of the radiation field and it is symmetric and trace-free (i.e. P
ij
= P
ji
and  = 0). Equation (2.34) holds in flat space-time. On the 2-sphere the line element can be written as
= 0). Equation (2.34) holds in flat space-time. On the 2-sphere the line element can be written as

The polarization matrix P ij will now be generalized as

satisfying P
ab
= P
ba
, and gabP
ab
= 0, where  is a unit vector in the direction (ϑ, φ). The sign of the off-diagonal entries in Eq. (2.81) is opposite with respect to the one obtained in Eq. (2.34). This is just because we want to match with the conventions adopted, for instance, in [100–102]. To avoid possible confusions, furthermore, the Latin indices a, b, c, d, .... run over the two-dimensional space.
is a unit vector in the direction (ϑ, φ). The sign of the off-diagonal entries in Eq. (2.81) is opposite with respect to the one obtained in Eq. (2.34). This is just because we want to match with the conventions adopted, for instance, in [100–102]. To avoid possible confusions, furthermore, the Latin indices a, b, c, d, .... run over the two-dimensional space.
As already mentioned, for scalar functions defined on the 2-sphere, such as the temperature anisotropies, the spherical harmonic functions Yℓm( ) are the complete orthonormal basis. For the 2 × 2 tensors defined on the 2-sphere, such as P
ab
in Eq.(2.81), the complete orthonormal set of tensor spherical harmonics can be written as [100–102]:
) are the complete orthonormal basis. For the 2 × 2 tensors defined on the 2-sphere, such as P
ab
in Eq.(2.81), the complete orthonormal set of tensor spherical harmonics can be written as [100–102]:


where ∇, in this subsection, denotes a covariant derivation on the 2-sphere, e.g.


Using Eq. (2.80) into Eq. (2.85), the Christoffel connections  on the 2-sphere are
on the 2-sphere are

In Eq. (2.83) the normalization factor is given by  , while
, while

is the Levi-Civita symbol on the 2-sphere. Notice that Nℓ differs from  defined in Eqs. (2.46) (see also Eqs. (2.63) and (2.64)) by a factor
defined in Eqs. (2.46) (see also Eqs. (2.63) and (2.64)) by a factor  . This difference will be ultimately relevant to relate
. This difference will be ultimately relevant to relate  and
and  .
.
The differential operators acting in Eqs. (2.82) and (2.83) are interpreted as a generalized gradient and curl operators, i.e.

The explicit form of the various components of  and
and  can be computed. For instance using Eqs. (2.82), (2.84) and (2.86), the explicit components of
can be computed. For instance using Eqs. (2.82), (2.84) and (2.86), the explicit components of  :
:



The expressions obtained in Eqs. (2.89), (2.90) and (2.91) can be simplified by recalling Eqs. (2.74), (2.75) and (2.79). Equations (2.89), (2.90) and (2.91) can be simply rewritten as



The same exercise can be conducted for the various components of  . The
. The  and
and  can be written in the form of 2 × 2 matrices:
can be written in the form of 2 × 2 matrices:

and as

where

In terms of the spin-2 harmonics ±2Y(lm)( )
)

which is Eq. (2.58). Using the orthonormality of the spherical harmonics Yℓm( ) it is easy to prove the orthonormality conditions, i.e.
) it is easy to prove the orthonormality conditions, i.e.

where d = sin ϑdϑdφ denotes, as usual, the integration over the solid angle. Since
= sin ϑdϑdφ denotes, as usual, the integration over the solid angle. Since  and
and  form an appropriate orthonormal basis, the polarization can be expanded as
form an appropriate orthonormal basis, the polarization can be expanded as

where expansion coefficients  and
and  represent the electric and magnetic type components of the polarization, respectively. Note that the sum starts from ℓ = 2, since relic gravitons generate only perturbations of multipoles from the quadrupoles up. The expansion coefficients are obviously
represent the electric and magnetic type components of the polarization, respectively. Note that the sum starts from ℓ = 2, since relic gravitons generate only perturbations of multipoles from the quadrupoles up. The expansion coefficients are obviously

In the notations of [98] the  and
and  can be related to the
can be related to the 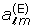 and
and  already introduced in Eq. (2.68). The relation between the two sets of expansion coefficients is simply:
already introduced in Eq. (2.68). The relation between the two sets of expansion coefficients is simply:

The two approaches to the spin weighted spherical harmonics described in the present section are equivalent and can be used interchangeably depending upon the specific problem.
3 The action of the relic gravitons
3.1 Second-order fluctuations of the Einstein-Hilbert action
By perturbing the Einstein-Hilbert action, to second-order in the amplitude of the tensor fluctuations we have, formally, that:

where  denotes the background Ricci scalar; δ(1)R and δ(2)R denote respectively, the first and second-order fluctuations of R = gμνR
μν
. In Eq. (3.1) the possible coupling to the anisotropic stress has been neglected. This is customary during the early evolution of the geometry since, in the context of the ΛCDM paradigm, during the early inflationary phase the sources of anisotropic stress can be safely ignored unless the number of effective e-folds is close to minimal. Later on the anisotropic stress of the fluid plays a role and cannot be neglected at least if we aim at a reasonable quantitative discussion of the relic graviton spectrum (see also section 1 and Fig. 3). By introducing the first-order fluctuations of the background geometry
denotes the background Ricci scalar; δ(1)R and δ(2)R denote respectively, the first and second-order fluctuations of R = gμνR
μν
. In Eq. (3.1) the possible coupling to the anisotropic stress has been neglected. This is customary during the early evolution of the geometry since, in the context of the ΛCDM paradigm, during the early inflationary phase the sources of anisotropic stress can be safely ignored unless the number of effective e-folds is close to minimal. Later on the anisotropic stress of the fluid plays a role and cannot be neglected at least if we aim at a reasonable quantitative discussion of the relic graviton spectrum (see also section 1 and Fig. 3). By introducing the first-order fluctuations of the background geometry  we have that
we have that



Recalling now Eqs. (2.1) and (2.8), Eqs. (3.2)-(3.4) become

The first- and second-order fluctuations of the Christoffel connections are:

where the prime denotes a derivation with respect to the conformal time coordinate. Using the result of Eq. (3.6) the first- and second- order fluctuations of the Ricci tensor can be written in explicit terms:



The Ricci scalar is zero to first order in the tensor fluctuations, i.e.  R = 0. This is due to the traceless nature of these fluctuations. To second-order, however,
R = 0. This is due to the traceless nature of these fluctuations. To second-order, however,  R ≠ 0 and its form is:
R ≠ 0 and its form is:

Using the results of Eqs. (3.7)-(3.10) into Eq. (3.1) the second-order action for the tensor modes reads, up total derivatives,

where, as already mentioned in section 1,

3.2 Lagrangian densities
The action (3.11) can be written in various ways which differ by the addition (or subtraction) of a total conformal time derivative. Recalling the standard notations

the Langrangian density ℒ(1)( , τ) can be recast in the form
, τ) can be recast in the form

where the canonical amplitude h has been introduced

By now introducing the canonical amplitude as ah = μ, Eq. (3.13) can be transformed as

If a total τ derivative is dropped, an equivalent form of the Lagrangian density can be obtained

All the three Lagrangian densities of Eqs. (3.14), (3.16) and (3.17) lead to the same Euler-Lagrange equations.
3.3 Hamiltonian densities
In Eq. (3.14) the canonical field is h and the canonical momentum is Π = ah'. Conversely, in Eq. (3.16) the canonical field is μ and the associated canonical momentum is  = μ' - ℋμ. Finally, according to Eq. (3.17) the canonical momentum is π = μ' while the canonical field is always μ. The three Lagrangian densities of Eqs. (3.14), (3.16) and (3.17) will then lead to three corresponding Hamiltonians, i.e.
= μ' - ℋμ. Finally, according to Eq. (3.17) the canonical momentum is π = μ' while the canonical field is always μ. The three Lagrangian densities of Eqs. (3.14), (3.16) and (3.17) will then lead to three corresponding Hamiltonians, i.e.



The Hamiltonians of Eqs. (3.18), (3.19) and (3.20) are related by successive canonical transformations. To prove this statement it is enough to show that Eq. (3.19) can be obtained from Eq. (3.18) by means of an appropriate canonical tansformation and that, in turn, Eq. (3.20) can be obtained from Eq. (3.19) through another canonical transformation. To pass from the Hamiltonian of Eq. (3.18) to Eq. (3.19) it is practical to consider a generating functional depending upon the new canonical fields (i.e. μ) and upon the old canonical momenta (i.e. Π):

By taking the functional derivative of  with respect to Π and with respect to μ we get, up to a sign, the connection between the new and old pivot variables, namely:
with respect to Π and with respect to μ we get, up to a sign, the connection between the new and old pivot variables, namely:

Since the generating functional depends explicitly upon time, the new Hamiltonian will be related to the old one through a partial time derivative of the generating functional, i.e.

as it can be explicitly verified by using Eqs. (3.18), (3.19) and (3.21) into Eq. (3.23). A further canonical transformation allows to go from Eq. (3.19) to (3.20); the relevant generating functional is

depending upon the old coordinates (i.e. μ) and upon the new momenta (i.e. π). The relations between the new and old variables are given by

stipulating that, in this case, the canonical momentum gets shifted by ℋμ while the canonical field is left invariant. Since the generating functional depends explicitly upon the conformal time coordinate, we will simply have that

as it can be explicitly verified by using Eqs. (3.19), (3.20) and (3.25) into Eq. (3.26).
3.4 Evolution equations in different regimes
From Eq. (3.11) the evolution equations of  will be given by
will be given by

The canonical field h (see Eq. (3.15)) will also obey Eq. (3.27). The Hamilton equations derived from Eq. (3.18) read:

which has exactly the same content as Eq. (3.27). In similar terms the Hamilton's equations can be derived from Eq. (3.19) and the result is

Bearing in mind that ah = μ, Eqs. (3.28) and (3.29) all reduce to Eq. (3.27) since the different Hamiltonians are related by canonical transformations. The same conclusion follows by deriving the Hamilton's equations using Eq. (3.20). It is practical, for some applications, to change the time parametrization. For instance, in terms of the rescaled time coordinate σ we will have that the evolution for the canonical amplitude h obeys the simple equation

Before concluding this section it should be pointed out that Eq. (3.27) is accurate as long as the sources of anisotropic stress are totally absent. This approximation is, strictly speaking, unrealistic. Indeed we do know that there are sources of anisotropic stress. Typically, after neutrino decoupling, the neutrinos free stream and the effective energy-momentum tensor acquires, to first-order in the amplitude of the plasma fluctuations, an anisotropic stress, i.e.

where  is the contribution of the anisotropic stress, satisfying
is the contribution of the anisotropic stress, satisfying  and
and  = 0. The presence of the anisotropic stress clearly affects the evolution of the tensor modes. To obtain the wanted equation we perturb the Einstein equations to first-order and we get:
= 0. The presence of the anisotropic stress clearly affects the evolution of the tensor modes. To obtain the wanted equation we perturb the Einstein equations to first-order and we get:

This form of the evolution equation for the tensor modes is the one required to compute the effects related to the finite value of the anisotropic stress.
4 Quantization of the tensor modes
There are analogies between the quantum state of relic gravitons and the quantum treatment of visible light. Quantum effects are not crucial to treat first-order interference of the radiation field (i.e. Young interferometry) [104]. First-order interference in quantum optics correspond to the calculation of the two-point function of the relic gravitons. Quantum effects arise, in optics, from second-order interference, i.e. when computing (and measuring) the interference between the intensities of the radiation field. Second-order interference effects are associated with the possibilities of counting photons and have been pioneered by Hanbury-Brown and Twiss in the early fifties [104, 105]. Hanbury-Brown-Twiss interferometry is based on photon counting statistics.
Having said that we are not even close (experimentally) to study graviton counting statistics (as we do it with the photons), second order interference effects would allow, in principle, to assess the coherence properties of relic graviton backgrounds. The quantum state of the relic gravitons can be described in terms of a generalized coherent state usually called squeezed state. Squeezed states can be described in terms of quadrature operators where one of the modes of the radiation field is always broadened by the time evolution, while the other one is squeezed.
4.1 Heisenberg description
The quantization of the canonical Hamiltonian of Eq. (3.20) is performed by promoting the normal modes of the action to field operators in the Heisenberg description and by imposing (canonical) equal-time commutation relations:

The operator corresponding to the Hamiltonian (3.20) becomes:

In Fourier space the quantum fields  and
and  can be expanded as
can be expanded as

Demanding the validity of the canonical commutation relations of Eq. (4.1), the Fourier components must obey:

Inserting now Eq. (4.3) into Eq. (3.20) the Fourier space representation of the quantum Hamiltonian can be obtained:

To derive Eq. (4.5) the relations  and
and  should be used. The evolution of
should be used. The evolution of  and
and  is therefore dictated, in the Heisenberg representation, by:
is therefore dictated, in the Heisenberg representation, by:

where, as usual, units ħ = 1 are assumed. Using now the mode expansion (4.3) and the Hamiltonian in the form (4.5) the evolution for the Fourier components of the operators is

implying

It is not a surprise that the evolution equations of the field operators, in the Heisenberg description, reproduces, for  the classical evolution equation derived before. The general solution of the system is then
the classical evolution equation derived before. The general solution of the system is then


where the mode functions obey:

If the form of the Hamiltonian is different by a time-dependent canonical transformation, also the canonical momenta will differ and, consequently, the relation of g to f may be different. For instance, in the case of the Hamiltonian of Eq. (3.19) we will have, instead,

Consider now the canonical commutation relations expressed by Eq. (4.1). Using Eqs. (4.3) together with Eqs. (4.9) and (4.10) into Eq. (4.1), the mode functions have to obey the condition:

Since, by construction, the Hamiltonians of Eqs. (3.19) and (3.20) are related by canonical transformations, the mode functions of Eqs. (4.11) and (4.12) will have both to obey Eq. (4.13). In different terms, the commutation relations between field operators should be preserved by the time evolution and this is equivalent to the Wronskian normalization condition of Eq. (4.13).
4.2 Generalized coherent states of relic gravitons
Consider the Hamiltonian given in Eq. (3.19) in the spatially flat case:

dropping, for simplicity, the tilde from the momenta. Defining the creation and annihilation operators

and recalling that  and
and  , Eq. (4.15) imply
, Eq. (4.15) imply

Since  and
and  obey
obey  , inserting Eq. (4.16) into Eq. (4.14),
, inserting Eq. (4.16) into Eq. (4.14),  can be written as
can be written as

The evolution of  and
and  obeys:
obeys:

The solution of Eq. (4.18) is:


where τ0 is the initial integration time. The unitarity of the time evolution demands that |u k (τ)|2-|v k (τ)|2 = 1. A useful parametrization of u k (τ) and v k (τ) is given in terms of a real amplitude and two phases as:

Equation (4.18) determine the evolution equations for u k (τ) and v k (τ). Using then Eq. (4.21) the evolution equations for r k , φ k and ϑ k can be obtained:



Note that ϑ
k
does not appear neither in Eq. (4.22) nor in Eq. (4.23). It is interesting, at this point, to compute the two-point functions connected with the two canonically conjugate operators, i.e.  (
( , τ) and
, τ) and  (
( , τ). In terms of the creations and annihilations operators defined in Eqs. (4.15) and (4.16)-(4.17) the canonically conjugate operators can be written as
, τ). In terms of the creations and annihilations operators defined in Eqs. (4.15) and (4.16)-(4.17) the canonically conjugate operators can be written as


There is a slight difference in the normalizations adopted between Eqs. (4.9)-(4.10) and Eqs. (4.25)-(4.26). This difference is due to the fact that, in Eqs. (4.9)-(4.10) the mode functions f
k
are normalized, asymptotically, in such a way that f
k
→ 1/ . In Eqs. (4.15)-(4.16) the factors
. In Eqs. (4.15)-(4.16) the factors  and
and  have been included in the definition creation and annihilation operators.
have been included in the definition creation and annihilation operators.
After simple calculations the two-point functions of the field operators and of their related canonical momenta becomes:


where r =  . Again, as already remarked, the non-strandard pre-factors apperaing in the Fourier amplitudes of Eqs. (4.27) and (4.28) are a consequence of the normalizations of Eq. (4.15). In the limit
. Again, as already remarked, the non-strandard pre-factors apperaing in the Fourier amplitudes of Eqs. (4.27) and (4.28) are a consequence of the normalizations of Eq. (4.15). In the limit  → 0 (and making use of the definitions of Eq. (4.21)), Eqs. (4.27) and (4.28) lead to
→ 0 (and making use of the definitions of Eq. (4.21)), Eqs. (4.27) and (4.28) lead to


Equations (4.29) and (4.30) show that the canonical field is broadened while the conjugate momentum gets squeezed by keeping constant the product of their respective root mean squares. The latter behaviour is evident as soon as the relevant wavelengths are larger than the Hubble radius. To demonstrate the two previous statements consider, indeed, Eqs. (4.22) and (4.23). Their solution for wavelengths larger than the Hubble radius (i.e. to leading order in kτ < 1) is:

Using Eq. (4.31) into Eqs. (4.29) and (4.30) we do get


The rationale for the behaviour exhibited by Eq. (4.31) can be understood also from a slightly different perspective. The relation between u k (τ) and v k (τ) and the tensor mode functions f k (τ) and g k (τ) is

where the evolution of f k (τ) and g k (τ) is obtained by solving Eq. (4.12). Indeed, by solving Eq. (4.12) in the limit k2 ≪ (ℋ2 + ℋ') we get

From Eq. (4.35) the first derivative of f k with respect to τ is nothing but

By computing g k (τ) from Eq. (4.35) it is clear that, in the limit kτ ≪ 1

which has exactly the same physical content of Eqs. (4.32) and (4.33). When the Universe expands, g k (τ) decreases and that the solution associated with A2(k) becomes progressively subleading. However, this observation does not imply that g k (τ) disappears since the evolution must be unitary. This feature of squeezed quantum state suggests the possibility of associating an effective entropy to the process of graviton production[106–110].
In the Schrödinger description quantum state of the relic gravitons is closely related to the squeezed states of the radiation field [111] (see also [112, 113]). Defining, for practical reasons,

the wavefunction of the ground state will be, for a given mode k,

where, as previously discussed, φ k → 0 has been assumed. In Eq. (4.39) Σ k (r k , φ k ) is the so-called two-mode squeezing operator [114, 115] which will now be written in its generic form:

where the creation and destruction operators are the ones computed in τ0, i.e.  by definition of Schrödinger description. The state |0⟩ is annihilated both by
by definition of Schrödinger description. The state |0⟩ is annihilated both by  and by
and by  . These two-modes appear simultaneously since gravitons are produced from the vacuum whose total momentum vanish. The x and
. These two-modes appear simultaneously since gravitons are produced from the vacuum whose total momentum vanish. The x and  have been dubbed, in the literature, as superfluctuant operators (see, e. g., [106–108]).
have been dubbed, in the literature, as superfluctuant operators (see, e. g., [106–108]).
The statistical properties of squeezed states can be addressed by employing a useful analogy with quantum optics. The idea is to pretend to resolve single gravitons and to study the statistical properties of the second-order interference effects. In the case of the gravitons this problem is addressed by defining the (normalized) Glauber correlation function not for the photons (as customarily done) but for the gravitons. For simplicity let us consider a single mode of the field. In this case the normalized Glauber intensity correlation can be written as

the colons denote normal ordering and  denotes the operator corresponding to the intensity of the radiation field. The normal ordering is related to the fact that, in the optical domain, most measurements of the electromagnetic field are based on the absorption of photons via the photoelectric effect. Needless to say that there is no analog of photoelectric detection for (single) relic gravitons. In this sense the following considerations should be regarded as a conditional predictions based on the analogy between squeezed states of photons and squeezed states of gravitons.
denotes the operator corresponding to the intensity of the radiation field. The normal ordering is related to the fact that, in the optical domain, most measurements of the electromagnetic field are based on the absorption of photons via the photoelectric effect. Needless to say that there is no analog of photoelectric detection for (single) relic gravitons. In this sense the following considerations should be regarded as a conditional predictions based on the analogy between squeezed states of photons and squeezed states of gravitons.
In the case of a single mode of the field Eq. (4.41) can also be written as

In Eq. (4.42) the normalized two point function is written for coincident spatial points (i.e. Δt = 0). The Hanbury-Brown and Twiss experiment, in some sense, probes directly the properties of g(2)(0). In the case of coherent states, g2(0) = 1: this is the case when the photoelectric counts obey a Poisson statistics. In the case of chaotic light, the joint detection probability greater than that for two independent events. This can be verified from Eq. (4.42) by assuming that the state of the photons/gravitons is given by a thermal mixture. Equation (4.42) can also be recast in the form

where  is the photon number variance and
is the photon number variance and  . From Eq. (4.43) it is also customary to define the Mandel's Q-parameter, i.e.
. From Eq. (4.43) it is also customary to define the Mandel's Q-parameter, i.e.

which vanishes exactly in the case of a coherent state. The latter statement can be easily appreciated since, for a coherent state,  . Thus,
. Thus,  . In the case of chaotic (thermal) light it turns out that g(2)(0) = 2. This result can be easily drived by using the so-called Glauber-Sudarshan P-representation of the density matrix, i.e.
. In the case of chaotic (thermal) light it turns out that g(2)(0) = 2. This result can be easily drived by using the so-called Glauber-Sudarshan P-representation of the density matrix, i.e.

where  is the Bose-Einstein occupation number. In the P-representation we have that
is the Bose-Einstein occupation number. In the P-representation we have that

where ⟨|α|2⟩ = ∫d2 α|α|2 P(α). By performing the required integrations it is easy to show that g(2)(0) - 1 = 1, i.e. g(2)(0) = 2. So far it has been shown that while a purely coherent state implies g(2) = 1 (i.e. Poissonian statistic) a thermal state implies that g(2)(0) = 2. In the case of the squeezed states it can be shown that

where ⟨ ⟩ = sinh2 r
k
is the multiplicity. The coherent state leads to a radiation field with Poissonian statistics. Thermal states (as well as squeezed states) have a statistics which is, according to the quantum optical terminology, superpoissonian. The latter statement is often dubbed by saying that if g(2)(0) > 1 photons are bunched while, in the opposite case (i.e. g(2)(0) < 1) the photons are said to be anti-bunched. The quantum optical language is much more effective for a mathematical description of the semi-classical limit than the usual considerations related to the limit ħ → 0. Squeezed states are genuine quantum states with many particles. They are, in some sense, like coherent states with the crucial difference that their statistics is super-Poissonian. The possibility of scrutinizing the statistical properties of many-gravitons systems would rely on our ability of resolving single gravitons which is not even close to the present technological capabilities.
⟩ = sinh2 r
k
is the multiplicity. The coherent state leads to a radiation field with Poissonian statistics. Thermal states (as well as squeezed states) have a statistics which is, according to the quantum optical terminology, superpoissonian. The latter statement is often dubbed by saying that if g(2)(0) > 1 photons are bunched while, in the opposite case (i.e. g(2)(0) < 1) the photons are said to be anti-bunched. The quantum optical language is much more effective for a mathematical description of the semi-classical limit than the usual considerations related to the limit ħ → 0. Squeezed states are genuine quantum states with many particles. They are, in some sense, like coherent states with the crucial difference that their statistics is super-Poissonian. The possibility of scrutinizing the statistical properties of many-gravitons systems would rely on our ability of resolving single gravitons which is not even close to the present technological capabilities.
5 Relic graviton backgrounds: observables
In the literature relic graviton backgrounds are characterized in terms of different quantities and, in particular, the most common ones are:
-
the power spectrum
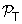 (k, τ);
(k, τ); -
the spectral energy density of the relic gravitons ΩGW(k, τ);
-
the spectral amplitude
 (ν, τ).
(ν, τ).
It is understood that all the mentioned quantities can be expressed either in terms of the wave-number or in terms of the frequency since k = 2πν.
The three listed variables can be related in different regimes. For instance the power spectrum has a simple relation to the spectral energy density when the relevant wavelengths are inside the Hubble radius. In section 6 it will be argued that, for numerical applications, the transfer function for the spectral energy density is more practical to compute than the transfer function for the power spectrum or for the spectral amplitude itself. The power spectrum is actually a strongly oscillating function of the conformal time coordinate for wavelengths shorter than the Hubble radius (i.e. kτ > 1); in the same limit the spectral energy density is asymptotically constant.
5.1 The tensor power spectrum and the spectral amplitude
The two-point function of the tensor modes of the geometry is defined as:

where the state |0⟩ is annihilated by  for λ = ⊗, ⊕. Recalling Eqs. (2.9) and (4.3),
for λ = ⊗, ⊕. Recalling Eqs. (2.9) and (4.3),  , the expansion of
, the expansion of  will then be:
will then be:

where ϵ
ij
( ) has been defined in Eqs. (2.10)-(2.11) and where
) has been defined in Eqs. (2.10)-(2.11) and where

In Eq. (5.2) Fk, λ(and the associated Gk, λ) are the (complex) tensor mode functions obeying

It is immediate to realize that

where fk, λand gk, λhave been introduced, for a single graviton polarization, in Eqs. (4.10)-(4.11). After computing the expectation value we get:

which, thanks to spatial isotropy, can also be written as:

where 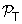 (k, τ) is, by definition, the tensor power spectrum:
(k, τ) is, by definition, the tensor power spectrum:

In Eq. (5.7), 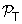 (k, τ) is the tensor power spectrum which has been implicitly introduced in Eq. (1.2) when talking about the customary parametrization of tensor power spectra in the context of the ΛCDM model. It is often useful, for practical applications, to consider h
ij
(
(k, τ) is the tensor power spectrum which has been implicitly introduced in Eq. (1.2) when talking about the customary parametrization of tensor power spectra in the context of the ΛCDM model. It is often useful, for practical applications, to consider h
ij
( , τ) as a classical field characterized by a Fourier amplitude obeying a specific stochastic average. Then we can write
, τ) as a classical field characterized by a Fourier amplitude obeying a specific stochastic average. Then we can write

where the Fourier amplitudes obey:

Following the suggestions of [98], it is useful to introduce, for some applications the stochastic fields

Equation (5.10) implies that


where 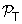 (k) denotes the tensor power spectrum and where the factor 2 in front of the averages arises as a consequence of the
(k) denotes the tensor power spectrum and where the factor 2 in front of the averages arises as a consequence of the  appearing in Eq. (5.11). In Eqs. (5.11), (5.12) and (5.13) the conformal time coordinate is absent. In Eq. (5.10) the conformal time appears explicitly. Indeed, Eqs. (5.11), (5.12) and (5.13) tacitly assume that h⊕(
appearing in Eq. (5.11). In Eqs. (5.11), (5.12) and (5.13) the conformal time coordinate is absent. In Eq. (5.10) the conformal time appears explicitly. Indeed, Eqs. (5.11), (5.12) and (5.13) tacitly assume that h⊕( , τ) = e⊕(
, τ) = e⊕( )Te(k, τ) and that h⊗(
)Te(k, τ) and that h⊗( , τ) = e⊗(
, τ) = e⊗( )Te(k, τ). This factorization is related to the concept of transfer function for the amplitude which will be discussed in section 6. The decomposition of Eqs. (5.11), (5.12) and (5.13) is useful when all the polarization have to be treated simultaneously typically in problems involving long wavelength gravitons (see Eqs. (7.85)-(7.86) and discussion therein). Furthermore the decomposition of Eqs. (5.11), (5.12) and (5.13) allows to factorize the dependence upon the initial spectrum which is useful for numerical applications.
)Te(k, τ). This factorization is related to the concept of transfer function for the amplitude which will be discussed in section 6. The decomposition of Eqs. (5.11), (5.12) and (5.13) is useful when all the polarization have to be treated simultaneously typically in problems involving long wavelength gravitons (see Eqs. (7.85)-(7.86) and discussion therein). Furthermore the decomposition of Eqs. (5.11), (5.12) and (5.13) allows to factorize the dependence upon the initial spectrum which is useful for numerical applications.
It is finally common to characterize the stochastic backgrounds of relic gravitons in terms of the so-called spectral amplitude. The definition of the spectral amplitude can be read-off from the definition of 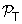 (k, τ). More precisely, taking the limit
(k, τ). More precisely, taking the limit  in Eq. (5.6) we will have that
in Eq. (5.6) we will have that

where the second equivalence defines the spectral amplitude  (ν) by recalling, once more, that the comoving wavenumber is related to the comoving frequency as k = 2πν.
(ν) by recalling, once more, that the comoving wavenumber is related to the comoving frequency as k = 2πν.
5.2 Energy-momentum tensors for the relic gravitons
According to Eq. (3.11), each polarization of the graviton obeys the action of a minimally coupled scalar field. This observation was discussed, in particular, in [116, 117] by Ford and Parker (see also, e.g. [54]). Following then Refs. [116, 117] and within our set of notations the energy-momentum tensor of the relic gravitons becomes

which can be obtained from the action of the gravitons by taking the functional derivative with respect to  . By making explicit the sum over the polarizations, Eq. (5.15) becomes:
. By making explicit the sum over the polarizations, Eq. (5.15) becomes:

i.e., even more explicitly,

By now using the same rescalings defined in Eq. (3.15) for h⊗ and h⊕ in terms of the canonical amplitude h we do get, from Eq. (5.17),

From Eq. (5.18) it is clear that the total energy momentum pseudo-tensor summed over the two polarizations of the graviton is twice the energy-momentum tensor of a minimally coupled scalar degree of freedom provided the amplitudes of the two polarizations are defined in terms of h as in Eq. (3.15). The (00) and (ij) components of the energy-momentum pseudo-tensor of Eq. (5.18) are:


where ∂ τ denotes a derivation with respect to the conformal time coordinate τ. Since, by definition,

the energy density and pressure of the relic gravitons can then be written as



The superscript in the energy density and pressure (i.e.  and
and  ) is convenient since different prescriptions for assigning the energy-momentum pseudo-tensor will be compared in a moment.
) is convenient since different prescriptions for assigning the energy-momentum pseudo-tensor will be compared in a moment.
The other possible definition of the energy-momentum pseudo-tensor stems from the generalization, to curved space-times, of the usual at space-time approach [118] (see also [119, 120]). The nonlinear corrections to the Einstein tensor, will consist, to lowest order, of quadratic combinations of h ij that can be formally expressed as

where the superscript at the right hand side denotes the second-order fluctuation of the corresponding quantity while the subscript refers to the tensor nature of the fluctuations. This procedure is essentially the one described in [119, 120] and has been re-explored, in a cosmological context, in [121, 122] (see also [123]). Recalling the form of the Einstein tensor [124],

we obtain

where  is a total derivative, i.e.
is a total derivative, i.e.

From Eqs. (3.9) and (3.10) it is also possible to write:

where  and
and  are further total derivative
are further total derivative

Therefore, up to total derivatives, the following result holds:

and

To pass from doubly covariant indices to mixed ones, it is useful to recall that, to second order,

By looking at the form of the specific terms arising in the previous equation it is clear that  and that
and that  . The expressions for
. The expressions for  and
and  are
are


where


with  . (see also Eqs. (5.36) and (5.37)). These expressions coincide with the ones obtained, for instance, in [121, 122] and are also consistent with the ones of [119, 120]. From Eqs. (5.34) and (5.36) the components of the energy and pressure density can be easily obtained since, by definition,
. (see also Eqs. (5.36) and (5.37)). These expressions coincide with the ones obtained, for instance, in [121, 122] and are also consistent with the ones of [119, 120]. From Eqs. (5.34) and (5.36) the components of the energy and pressure density can be easily obtained since, by definition,  and
and  . As discussed in Eqs. (5.16)-(5.23) it is rather useful to derive the explicit form of
. As discussed in Eqs. (5.16)-(5.23) it is rather useful to derive the explicit form of  and
and  in terms of the normalized canonical amplitude defined in Eq. (3.15). The result of this calculation is simply:
in terms of the normalized canonical amplitude defined in Eq. (3.15). The result of this calculation is simply:


By comparing Eqs. (5.38)-(5.39) with Eqs. (5.22)-(5.23) we can remark that the first term appearing in Eq. (5.38) is absent from Eq. (5.22). Moreover, also  and
and  seems to be superfficially different. As it will be shown in a moment the equivalence of the two approaches is clear as soon as the relevant wavelengths are larger than the Hubble radius at a given time.
seems to be superfficially different. As it will be shown in a moment the equivalence of the two approaches is clear as soon as the relevant wavelengths are larger than the Hubble radius at a given time.
Before proceeding with this step, it is relevant to remark that the components of the energy-momentum pseudo-tensor given in Eqs. (5.34) and (5.35) are not covariantly conserved. However, since the Bianchi identity  should be valid to all orders, we will also have that:
should be valid to all orders, we will also have that:

whose explicit form is

Recalling now the components of the energy-momentum pseudo-tensor and the results for the fluctuations of the Christoffel symbols we have

that can also be written as

where

5.3 The energy density of the relic gravitons
By choosing the prescription of Eq. (5.19) the energy density of the relic gravitons will be given by:

The expectation values appearing in Eq. (5.45) can be computed in different ways. For instance, from Eqs. (4.3) and (4.9)-(4.10), Eq. (5.45)

where the functions f k (τ) and g k (τ) are the mode functions obeying:

If the energy momentum pseudo-tensor has the form derived in Eq. (5.34), then the energy density will have, apparently, a slightly different form:

From Eqs. (5.46) and (5.48) the corresponding critical fractions are

The two relevant physical limits are for modes inside the Hubble radius (i.e. kτ > 1) and for modes outside the Hubble radius (i.e. kτ < 1). If k/ℋ > 1, then f k (τ) will be, in the first approximation, plane waves and g k (τ) ≃ ± ikf k (τ). In this limit:


In the limit kτ > 1 we will have ℋ2 ≪ k2. Thus Eqs. (5.50) and (5.51) coincide (up to corrections  (ℋ2/k2)). In this limit it is also possible to express ΩGW(k, τ) solely in terms of the power spectrum.
(ℋ2/k2)). In this limit it is also possible to express ΩGW(k, τ) solely in terms of the power spectrum.
Indeed, since

we will also have


In the opposite limit, i.e. when the given wavelengths are smaller than the Hubble radius, the same analysis implies  . In short the idea is that, for kτ ≪ 1, g
k
= ℋf
k
; indeed, for kτ ≪ 1, Eq. (5.4) implies
. In short the idea is that, for kτ ≪ 1, g
k
= ℋf
k
; indeed, for kτ ≪ 1, Eq. (5.4) implies

where the second term (going as B
k
/a(τ)) in Eq. (5.55) is actually negligible for large times. Therefore, in the limit kτ ≪ 1 it can be easily shown that  . It is curious to notice that, up to a factor of 2, the first energy density (i.e. Eq. (5.46)) leads to the same value obtained for modes inside the Hubble radius. Therefore, for modes which are inside the Hubble radius:
. It is curious to notice that, up to a factor of 2, the first energy density (i.e. Eq. (5.46)) leads to the same value obtained for modes inside the Hubble radius. Therefore, for modes which are inside the Hubble radius:

Consequently, we can define the critical fraction of relic gravitons at a given time as

where, in the third equality it has been used that ℋ = aH. Recalling Eq. (5.14) we can also express the critical fraction of relic gravitons in terms of the spectral amplitude. Indeed, according to Eq. (5.14)

and, therefore,

As long as the relevant wavelengths are shorter than the Hubble radius at a given time, different prescriptions for assigning the energy-momentum pseudo-tensor lead to the same result (see also the discussion in section 6). In the opposite limit different choices may exhibit quantitative differences. The limit of short wavelengths in comparison with the Hubble radius is the relevant one when discussing wide-band interferometers. Conversely, the initial conditions for the CMB anisotropies are set when the relevant wavelengths are larger than the Hubble radius before equality.
6 Relic gravitons from the ΛCDM scenario
6.1 Inflationary power spectra
During the inflationary phase, the tensor power spectrum can be easily computed by solving Eq. (5.4):

where  is the Hankel function of first kind [125, 126] and where ϵ = -
is the Hankel function of first kind [125, 126] and where ϵ = - /H2. To pass from Eq. (5.4) to Eq. (6.1) it is useful to bear in mind the following pair of identities
/H2. To pass from Eq. (5.4) to Eq. (6.1) it is useful to bear in mind the following pair of identities

The second equality in Eq. (6.2) follows (after integration by parts) from the relation between cosmic and conformal times, i.e. a(τ)dτ = dt. By substituting Eq. (6.1) into Eq. (5.7) the standard expression of the tensor power spectrum can be obtained. In particular, when the relevant modes exited the Hubble radius during inflation the power spectrum becomes

where the small argument limit of the Hankel functions has been taken. In the slow-roll approximation,  ; then Eq. (6.3) implies that
; then Eq. (6.3) implies that

Within the present notations, as already established in Eq. (3.12),  .
.
The spectral index defined from Eq. (6.4) is, by definition,

where the second equality follows from the identities obeyed by the slow-roll parameters [127]. The tensor and scalar power spectra are customarily assigned at a reference scale (usually dubbed pivot scale):

where, by definition,  is the amplitude of the tensor power spectrum evaluated at the pivot scale kp. In the case of single-field inflationary models, the power spectrum computed at the pivot scale kp (i.e.
is the amplitude of the tensor power spectrum evaluated at the pivot scale kp. In the case of single-field inflationary models, the power spectrum computed at the pivot scale kp (i.e.  ) and the spectral index nT can be related. Bearing in mind that the power spectrum of curvature perturbations is given, in single field inflationary models, as [127]
) and the spectral index nT can be related. Bearing in mind that the power spectrum of curvature perturbations is given, in single field inflationary models, as [127]

the ratio between the tensor and the scalar power spectra is given by

Equation (6.8) implies, recalling Eq. (6.5), that rT = -8nT. Since there is a direct relation of the tensor spectral index to rT, the number of the parameters can be reduced from two to one. In Tabs. 1 and 2 the values of rT have been reported as they can be estimated in few different analyses of the cosmological data sets.
6.2 Transfer functions for inflationary power spectra
Equation (6.6) correctly parametrizes the spectrum only when the relevant wavelengths are larger than the Hubble radius before matter-radiation equality (i.e. kτ ≃ k/ℋ < 1 for τ <νeq). To transfer the spectrum inside the Hubble radius the procedure is to integrate numerically Eq. (5.4) (as well as Eqs. (2.2)-(2.4)) across the relevant transitions of the background geometry. While the geometry passes from inflation to radiation, Eq. (6.6) implies that the tensor mode function is constant if the wavelength associated with the given Fourier mode is larger than the Hubble radius at the corresponding epoch:

The term proportional to B
k
in Eq. (6.9) leads to a decaying mode and F
k
(τ) is therefore determined, for |kτ | ≪ 1, by the first term whose squared modulus coincides with the spectrum computed in Eq. (6.4) and parametrized as in Eq. (6.6). The latter statement is true if the inflationary phase is suddenly followed by the radiation dominated epoch since, during radiation, a(τ) ≃ τ. The situation can be different if, after inflation, a stiff age takes over. The stiffer case still compatible with causality (i.e. wt = 1) leads approximately to a scale factor a(τ) ≃  . In the latter situation the second term inflEq. (6.9) grows logarithmically and cannot be neglected in comparison with the constant contribution. The evolution of the background (i.e. Eqs. (2.2)-(2.4)) and of the tensor mode functions (i.e. Eq. (5.4)) should therefore be solved across the radiation matter transition and the usual approach is to compute the transfer function for the amplitude [128] i.e.
. In the latter situation the second term inflEq. (6.9) grows logarithmically and cannot be neglected in comparison with the constant contribution. The evolution of the background (i.e. Eqs. (2.2)-(2.4)) and of the tensor mode functions (i.e. Eq. (5.4)) should therefore be solved across the radiation matter transition and the usual approach is to compute the transfer function for the amplitude [128] i.e.

In Eq. (6.10),  (τ) denotes the approximate form of the mode function (holding during the matter-dominated phase); F
k
(τ) denotes, instead, the solution obtained by fully numerical methods. The averages appearing in Eq. (6.10) refer to the average over the oscillations: as the wavelengths are inside the Hubble radius, the solutions are all oscillating. The numerical average over the phases introduces some arbitrariness which can be cured by computing directly the transfer function for the spectral energy density.
(τ) denotes the approximate form of the mode function (holding during the matter-dominated phase); F
k
(τ) denotes, instead, the solution obtained by fully numerical methods. The averages appearing in Eq. (6.10) refer to the average over the oscillations: as the wavelengths are inside the Hubble radius, the solutions are all oscillating. The numerical average over the phases introduces some arbitrariness which can be cured by computing directly the transfer function for the spectral energy density.
The calculation of T h (k) requires a careful matching over the phases between the numerical and the approximate (but analytic) solution. After matter-radiation equality, the scale factor is going, approximately, as a(τ) ≃ τ2 and, therefore, the (approximate) solution of Eq. (5.4) is given by

which is constant for kτ < 1. The result of the numerical integration for the amplitude transfer function  has been recently revisited in [46, 47] and it turns out to be
has been recently revisited in [46, 47] and it turns out to be

where

The latter result agrees with the findings of [128] who obtain  = 1.34 and
= 1.34 and  = 2.50. The value of keq can be obtained directly from the experimental data (see, for instance, last column of Tabs. 1 and 2 implying keq ≃
= 2.50. The value of keq can be obtained directly from the experimental data (see, for instance, last column of Tabs. 1 and 2 implying keq ≃  (0.009) Mpc-1). The WMAP 5-yr data combined with the supernova data and with the large-scale structure data would give
(0.009) Mpc-1). The WMAP 5-yr data combined with the supernova data and with the large-scale structure data would give  . A rather good analytic estimate for keq is
. A rather good analytic estimate for keq is

where the typical value selected for  is given by the sum of the photon component (i.e.
is given by the sum of the photon component (i.e.  = 2.47 × 10-5) and of the neutrino component (i.e.
= 2.47 × 10-5) and of the neutrino component (i.e.  = 1.68 × 10-5): the neutrinos, consistently with the ΛCDM paradigm, are taken to be massless and their (present) kinetic temperature is just a factor (4/11)1/3 smaller than the (present) photon temperature.
= 1.68 × 10-5): the neutrinos, consistently with the ΛCDM paradigm, are taken to be massless and their (present) kinetic temperature is just a factor (4/11)1/3 smaller than the (present) photon temperature.
Equation (6.14) stems from the observation that the exact solution of Eqs. (2.2)-(2.4) for the matter-radiation transition can be given as a(τ) = aeq [y2 + 2y] where y = τ/τ1. The time-scale τ1 = τeq( + 1) is related to the equality time τeq which can be estimated as
+ 1) is related to the equality time τeq which can be estimated as

In the case of the WMAP 5-yr data combined with the supernova and large-scale structure data  . Consequently, Eqs. (6.10), (6.11) and (6.12) imply that the spectrum of the tensor modes is given, at the present time, as
. Consequently, Eqs. (6.10), (6.11) and (6.12) imply that the spectrum of the tensor modes is given, at the present time, as

Within the standard approach, Eq. (6.16) is customarily connected to the spectral energy density of the relic gravitons. In [46, 47] it has been observed that it is simpler and more accurate to compute directly the transfer function for the spectral energy density. In the following subsection this procedure will be illustrated in two different cases.
6.3 Transfer function for the spectral energy
Instead of computing the transfer function for the power spectrum it is more direct (and more accurate) to compute directly the spectral energy density and its related transfer function. As previously discussed there can be ambiguities in assigning the energy density because of possible different forms of the energy-momentum pseudo-tensor. In particular in Eqs. (5.46) and (5.48) two different expressions have been proposed on the basis of slightly different physical considerations. The result of the numerical calculation are reported in Fig. 5 in terms of  (derived from Eq. (5.46)) and in terms of the transfer function of the spectral energy density (denoted by T
ρ
(κ)). The quantities
(derived from Eq. (5.46)) and in terms of the transfer function of the spectral energy density (denoted by T
ρ
(κ)). The quantities  (and, analogously,
(and, analogously,  ) are defined as
) are defined as
The function given in Eq. (6.17) is numerically computed (plot at the left) for different values of κ and in the case of the radiation-matter transition. In the plot at the right the transfer function for the spectral energy is illustrated.


While Eq. (6.17) follows from Eq. (5.46), Eq. (6.18) follows from Eq. (5.48); Eqs. (6.17)-(6.18) are related to the spectral energy densities in critical units, i.e.

As a function of x = kτ and κ = k/keq, both  and
and  go to a constant value when the relevant modes are evaluated deep inside the Hubble radius. This occurrence allows to introduce the energy transfer function which is defined as:
go to a constant value when the relevant modes are evaluated deep inside the Hubble radius. This occurrence allows to introduce the energy transfer function which is defined as:

The specific form of the energy-momentum tensor is immaterial for the determination of  : different forms of the energy-momentum tensor of the relic gravitons will lead to the same result. This aspect can be appreciated by looking at Fig. 6 where
: different forms of the energy-momentum tensor of the relic gravitons will lead to the same result. This aspect can be appreciated by looking at Fig. 6 where  has been reported for κ = 10-2 (plot at the left) and for κ = 10-4 (plot at the right). The dashed and the dot-dashed curves (in both plots) correspond, respectively, to
has been reported for κ = 10-2 (plot at the left) and for κ = 10-4 (plot at the right). The dashed and the dot-dashed curves (in both plots) correspond, respectively, to  and to
and to  . The full line, in both plots, corresponds to the combination
. The full line, in both plots, corresponds to the combination

where c± (k) are the mixing coefficients which parametrize the solution for the tensor mode functions when the relevant wavelengths are, asymptotically, inside the Hubble radius, i.e.

In Eq. (6.22)  and
and  are the solutions to leading order in the limit kτ ≫ 1. From Eq. (6.22), c± (k) are given by
are the solutions to leading order in the limit kτ ≫ 1. From Eq. (6.22), c± (k) are given by

Using Eqs. (6.22)-(6.23), Eqs. (6.17)-(6.18) can be directly calculated in the limit x = kτ ≫ 1 with the result that

which proofs that the oscillating contributions are suppressed as  for xf ≫ 1. To get to the results illustrated in Figs. 5 and 6 the evolution equations of the mode functions have been integrated by setting initial conditions deep outside the Hubble radius (i.e. x = kτ ≪ 1), by following the corresponding quantities through the Hubble crossing (i.e. x ≃ 1) and then, finally, deep inside the Hubble radius (i.e. x ≫ 1). The integration of the mode functions is most easily performed in terms of
for xf ≫ 1. To get to the results illustrated in Figs. 5 and 6 the evolution equations of the mode functions have been integrated by setting initial conditions deep outside the Hubble radius (i.e. x = kτ ≪ 1), by following the corresponding quantities through the Hubble crossing (i.e. x ≃ 1) and then, finally, deep inside the Hubble radius (i.e. x ≫ 1). The integration of the mode functions is most easily performed in terms of  . Using
. Using  can be written as
can be written as

In the case of the conventional ΛCDM scenario, the Universe is suddenly dominated by radiation as soon as inflation ends. Equation (5.4) implies that F k is constant when kτ ≪ 1. The initial conditions are fixed by requiring that, at the initial time of the numerical integration,

In Figs. 5 and 5, xi = 10-5 even if, for practical reasons, the scale on the horizontal axis has been narrowed. Bearing in mind Eq. (6.15), we can also write, for xi ≪ 1,

To avoid unnecessary complications, the initial condition of the integrations illustrated in Figs. 5 and 6 have been set as  (xi) = xi, i.e. the initial spectrum has been rescaled. The transfer function, by definition, must always depend only on the dynamics of the transition and not upon the features (e.g slope, amplitude) of the initial power spectrum.
(xi) = xi, i.e. the initial spectrum has been rescaled. The transfer function, by definition, must always depend only on the dynamics of the transition and not upon the features (e.g slope, amplitude) of the initial power spectrum.
In the plot at the right of Fig. 5, the fit to the energy transfer function is reported with the full (thin) line on top of the diamonds defining the numerical points. The analytical form of the fit can then be written as:

Equation (6.28) permits the accurate evaluation of the spectral energy density of relic gravitons, for instance, in the minimal version of the ΛCDM paradigm.
Yet another relevant physical situation for the present considerations is the one where the back-ground geometry, after inflation, transits from a stiff epoch to the ordinary radiation-dominated epoch. In the primeval plasma, stiff phases can arise for various reasons. Zeldovich [129] (see also [130]) suggested this possibility in connection with the entropy problem. In [82–84, 74] it has been suggested that the stiff phase could take place after the inflationary phase with the main purpose of identifying a potential source of high-frequency gravitons. This possibility was also prompted by a possible post-inflationary dominance of a quintessence field.
The simplest consideration leading to the possibility of a post-inflationary phase stiffer than radiation is connected with our extreme ignorance of the thermal history of the Universe after inflation. In a model-independent approach, it is plausible to think that the onset of the radiation-dominance could be delayed. This may happen, in concrete models, for various reasons. One possibility could be that the inflaton field does not decay but rather changes its dynamical nature by acting as quintessence field [85] (see also [131]). In this kind of situations we are the geometry passes from a stiff phase where


to a radiation-dominated phase where cst = 1/41. Note that, according to Eqs. (6.29) and (6.30),  = wt iff the (total) barotropic index is constant in time. In the limiting case wt = 1 =
= wt iff the (total) barotropic index is constant in time. In the limiting case wt = 1 =  and the speed of sound coincides with the speed of light. As argued in [132], barotropic indices wt >1 would not be compatible with causality (see, however, [133]). The presence of a suitable stiff phase has been also discussed recently as an effective way of suppressing entropic fluctuations [134] which are observationally constrained by the WMAP 5-yr data.
and the speed of sound coincides with the speed of light. As argued in [132], barotropic indices wt >1 would not be compatible with causality (see, however, [133]). The presence of a suitable stiff phase has been also discussed recently as an effective way of suppressing entropic fluctuations [134] which are observationally constrained by the WMAP 5-yr data.
As in the case of the matter-radiation transition the transfer function only depends upon κ which is defined, this time, as κ = k/ks, where ks =  and τs parametrizes the transition time. A simple analytical form of the transition regime is given by
and τs parametrizes the transition time. A simple analytical form of the transition regime is given by

where, by definition, ρsi = ρs(τi) and ρRi = ρR(τi). Equation (6.31) is a solution of Eqs. (2.2)-(2.4) when the radiation is present together with a stiff component which has, in the case of Eq. (6.31) a sound speed which equals the speed of light. In the limit y → 0 the scale factor expands as a(y) =  while, in the opposite limit, a(y) ≃ y. In Fig. 7 (plot at the right) Δρ (κ, x) is illustrated for different values of κ. We shall not dwell here (again) about the possible different forms of the energy momentum pseudo-tensor: provided the energy density is evaluated deep inside the Hubble radius the different approaches to the energy density of the relic gravitons give the same result. The transfer function for the spectral energy density is numerically illustrated always in Fig. 7 (plot at the left). The semi-analytical form of the transfer function becomes, this time,
while, in the opposite limit, a(y) ≃ y. In Fig. 7 (plot at the right) Δρ (κ, x) is illustrated for different values of κ. We shall not dwell here (again) about the possible different forms of the energy momentum pseudo-tensor: provided the energy density is evaluated deep inside the Hubble radius the different approaches to the energy density of the relic gravitons give the same result. The transfer function for the spectral energy density is numerically illustrated always in Fig. 7 (plot at the left). The semi-analytical form of the transfer function becomes, this time,

where ks =  . The value of ks can be computed in an explicit model but it can also be left as a free parameter. Taking into account that the energy density of the inflaton will be exactly
. The value of ks can be computed in an explicit model but it can also be left as a free parameter. Taking into account that the energy density of the inflaton will be exactly  , the value of ks (as well as the duration of the stiff phase) will be determined, grossly speaking, by Hi/
, the value of ks (as well as the duration of the stiff phase) will be determined, grossly speaking, by Hi/ . In the context of quintessential inflation [85] (see also [83, 84]) ρRi ≃
. In the context of quintessential inflation [85] (see also [83, 84]) ρRi ≃  [135].
[135].
In Fig. (7) (plot at the left) the full line superimposed to the numerical points (illustrated by boxes) is the fit of Eq. (6.32).
6.4 Analytic results for the mixing coefficients
The analytic results for the mixing coefficients are rather useful to obtain the final expression of the various transfer functions. Indeed, defining as k* the typical wavenumber of the transition (e.g. k* = keq in the case of the radiation-mattter transition), the slope of the transfer function of the spectral energy density can analytically obtained in the limit κ ≫ 1. This observation helps when we have, for instance, to fit the numerical data points with an analytical expression which will however reproduce the data not only for κ > 1 (as Figs. 5 and 7 clearly show).
For illustration of the method it is practical to consider the transition from a generic accelerated phase to a decelerated stage of expansion. In this situation, by naming the transition point -τ1, the continuous and differentiable form of the scale factors can be written as:


where the scale factors are continuous and differentiable at the transition point which has been generically indicated as τ1. The pump fields of the tensor mode functions turn out to be:

The mode functions can then be written as:

where

The continuity of the tensor mode functions at the transition point

implies that the mixing coefficients are given by:

where, according to the notations previously established, y1 = y(-τ1) = (α/β)x1. The case α = β = 1 corresponds to a transition from the inflationary phase to a radiation-dominated phase. In this case we do know which are the mixing coefficients. The previous expressions give us:

which clearly agree with previous results [50, 54, 56]. In the case of Eq. (6.40) |c+(k)|2 - |c- (k)|2 = 1 and k4|c-(k)|2 is exactly scale-invariant. Another interesting situation is the one of the transition from inflation to stiff, i.e. β = 1, α = 1/2, y1 = x1/2 which leads to a logarithmic enhancement at small wavenumbers [82, 83]. In this situation the mixing coefficients can be written as:


The above result can be expanded in for x1 ≪ 1 and the result is:


The logarithms arising in Eqs. (6.43) and (6.44) explain why, in Eq. (6.32), the transfer function of the spectral energy density contains logarithms. In spite of the fact that semi-analytical estimates can pin down the slope of the transfer functions in different intervals, they are insufficient for a faithful account of more realistic situations where the slow-roll corrections are relevant and when other dissipative effects (such as neutrino fee streaming) are taken into account.
6.5 Exponential damping of the mixing coefficients
Consider the case of the ΛCDM paradigm where the inflationary epoch is almost suddenly followed by the radiation-dominated phase. By denoting the transition time as τi, it is plausible to think that all the modes of the field such that k > aiHi ≃  are exponentially suppressed [136, 137]. For the modes kτi > 1, the pumping action of the gravitational field is practically absent. There will be a given k, be it kmax, for which k ≃
are exponentially suppressed [136, 137]. For the modes kτi > 1, the pumping action of the gravitational field is practically absent. There will be a given k, be it kmax, for which k ≃  . The latter wavenumber is, in practice, the maximal k to be amplified and it can be estimated as:
. The latter wavenumber is, in practice, the maximal k to be amplified and it can be estimated as:


Equations (6.45) and (6.46) are derived by assuming that, right after inflation, the radiation-dominated phase takes over. Furthermore, recalling the slow-roll dynamics,  and V ∝
and V ∝  . In Eqs. (6.45) and (6.46)
. In Eqs. (6.45) and (6.46)  denotes, as already established, the amplitude of the curvature power spectrum evaluated at the pivot scale.
denotes, as already established, the amplitude of the curvature power spectrum evaluated at the pivot scale.
By taking as typical values of the curvature perturbations at the pivot scale the one endorsed, for instance, by the WMAP 5-yr data alone we will have we will have that Eqs. (6.45) and (6.46) can be written as:

where the typical values of the slow-roll parameter have been derived by taking into account that, in the absence of running of the tensor spectral index, rT = 16ϵ; since, according to the WMAP 5-yr data alone, rT < 0.43, ϵ ≤ 0.01.
For phenomenological purposes it can be also interesting to know what kind of exponential suppression we can expect. From the analysis of various transitions it emerges that the mixing coefficients for k > kmax (or ν > νmax) will satisfy

From Eq. (6.48) we can easily argue that, for k > kmax, |c+(k)| → 1 and |c-(k)| ≃ 2-1/2 exp [-βk/kmax]. The point is then to estimate the value of β which depends on the nature of the transition regime (Fig. 8). Typically, however, β > 2 for sufficiently smooth transitions. To justify this statement it is interesting to consider the following toy model where the scale factor interpolates between a quasi-de Sitter phase and a radiation-dominated phase:

For τ → -∞ (i.e. τ ≪ -τi), a(τ) ≃ -ai/τ and the quasi de-Sitter dynamics is recovered. In the opposite limit (i. e. τ ≫ +τi), a(τ) ≃ ai τ and the radiation dominance is recovered. In Fig. 6 (plot at the left) the exponential damping of the mixing coefficients is numerically illustrated. The curve at the top (full line) illustrates the case κ = 1. The cases κ = 2 and κ = 3 are barely distinguishable at the bottom of the plot. Notice, always in the right plot, the rather narrow range of times which are reported in a linear scale. In the plot at the right the asymptotic values of the mixing coefficients are reported for different values of κ = k/kmax. By fitting the numerical data with with an equation of the form given in Eq. (6.48), the value of β = 6.33. Different examples can be presented on the same line of the one discussed in Fig. 6. While it is pretty clear that the decay is indeed exponential, the value of β may well vary. This can be summarized, for instance, in a rescaling of kmax, i.e. by positing, for instance that kmax →  /β. Thus, the dynamics of the transition can slightly shift the numerical value of the upper cut-off by a numerical factor which depends upon the width of the transition regime.
/β. Thus, the dynamics of the transition can slightly shift the numerical value of the upper cut-off by a numerical factor which depends upon the width of the transition regime.
6.6 Nearly scale-invariant spectra
By using the transfer function for the tensor amplitude, the spectral energy density for frequencies ν ≫ νeq can be simply given by:


where dA(z*) is the (comoving) angular diameter distance to decoupling. In Eqs. (6.50)-(6.51) (as well as in the program used for the numerical calculations) there are two complementary options. The first one is to use the angular diameter distance to decoupling which is directly inferred from the CMB data. For instance, in the case of the 5-yr WMAP data alone, dA(z*) = 14115  . This is the strategy also adopted in other studies [138] (in connection, obviously, with earlier releases of WMAP data). At the same time it is also possible to take the best fit value of the total matter fraction (i.e. ΩM0 = 0.258 for the case of the WMAP 5-yr data alone) and compute the comoving angular diameter distance according to the well know expression for spatially at Universes:
. This is the strategy also adopted in other studies [138] (in connection, obviously, with earlier releases of WMAP data). At the same time it is also possible to take the best fit value of the total matter fraction (i.e. ΩM0 = 0.258 for the case of the WMAP 5-yr data alone) and compute the comoving angular diameter distance according to the well know expression for spatially at Universes:

The latter strategy has been used, for instance, in [139]. The two strategies are compatible and, moreover, this explains why, in Eq. (6.51) the dependence upon ΩM0 does not cancel. In Eq. (6.50) nT denotes, as usual, the tensor spectral index which can be also written as

If αT = 0, the standard case is recovered. It should be finally mentioned that, in the limit ν ≫ νeq, the oscillating terms have to be appropriately averaged: this is done by setting the terms going as cos2 (2πν τ0) to 1/2. The latter procedure has been employed, for instance, in the analyses of [138, 44]. In Fig. 9 the transfer function for the spectral energy density (introduced in Eqs. (6.20) and (6.28)) has been consistently employed to estimate the spectral energy density itself and the spectral amplitude. According to Eq. (5.14) the spectral energy density can be written as

where we used that k = 2πν and that Ha = ℋ. By making explicit the numerical factors in Eq. (6.54), S h (ν, τ0) can be expressed in terms of the spectral energy (in critical units)

where, we recall, H0 = 3.24078 × 10-18 h0 Hz.
In Fig. 9 the spectral energy of the relic gravitons as well as S h (ν, τ0) are reported for different values of rT. The spectra of Fig. 9 have been obtained from the direct integration of the mode functions but can be parametrized, according to Eq. (6.28) as


By comparing Eqs. (6.50)-(6.51) to Eqs. (6.56)-(6.57), the amplitude for ν ≫ νeq differs, roughly, by a factor 2. This coincidence is not surprising since Eqs. (6.50)-(6.51) have been obtained by averaging over the oscillations (i.e. by replacing cosine squared with 1/2) and by imposing that |g k | = k|f k |. These manipulations are certainly less accurate than the procedure used to derive the transfer function for the spectral energy density.
So far the evolution of the tensor modes has been treated in the absence of anisotropic stress. This approximation is, strictly speaking, unrealistic. Indeed we do know that there are sources of anisotropic stress. After neutrino decoupling, the neutrinos free stream and the effective energy-momentum tensor acquires, to first-order in the amplitude of the plasma fluctuations, an anisotropic stress, i.e.

The presence of the anisotropic stress clearly affects the evolution of the tensor modes. To obtain the wanted equation we perturb the Einstein equations to first-order and we get:

Equation (6.59) reduces to an integro-differential equation which has been analyzed in [42] (see also [43–45]). The overall effect of collisionless particles is a reduction of the spectral energy density of the relic gravitons. Assuming that the only collisionless species in the thermal history of the Universe are the neutrinos, the amount of suppression can be parametrized by the function

where R ν is the fraction of neutrinos in the radiation plasma. In the case R ν = 0 (i.e. in the absence of collisionless patrticles) there is no suppression. If, on the contrary, R ν ≠ 0 the suppression can even reach one order of magnitude. In the case N ν = 3, R ν = 0.405 and the suppression of the spectral energy density is proportional to ℱ2(0.405) = 0.645. This suppression will be effective for relatively small frequencies which are larger than νeq and smaller than the frequency corresponding to the Hubble radius at the time of big-bang nucleosynthesis, i.e.

The effect of neutrino free-streaming (as well as all the other late time effects addressed in this subsection) has been taken into account in Fig. 2 (see section 1) but it is absent in Fig. 9. The second effect which has been taken into account in Fig. 2 is the damping associated with the (present) dominance of the dark energy component. Indeed the redshift of Λ-dominance is simply defined by

Consider now the mode which will be denoted as kΛ, i.e. the mode reentering the Hubble radius at τΛ. By definition kΛ = HΛ aΛ must hold. But for τ > τΛ is constant, i.e. HΛ ≡ H0 where H0 is the present value of the Hubble rate. Using now Eq. (6.62), it can be easily shown that kΛ = (ΩM0/ΩΛ)1/3 kH where kH = a0H0. The frequency interval between νH and νΛ is rather tiny. Indeed, it turns out that


For the same choice of parameters of Eq. (6.64), νH = 3.708 × 10-19 Hz which is not so different than νΛ = 2.607 × 10-19 Hz. It would therefore seem that this branch of the spectrum could be easily neglected. However, it turns out that the adiabatic damping of the mode function across τΛ reduces the amplitude of the spectral energy density by a factor (ΩM0/ΩΛ)2. For the typical choice of parameters of Eqs. (6.63) and (6.64) we have that the suppression is of the order of 0.12. Again this is a tiny number which is, anyway, comparable with the suppression due, for instance, to the neutrino free streaming. This class of effects has been repeatedly in a number of recent papers [140] (see also [141, 142]). The essence of the effect is captured by the following observation. Consider a mode k which reenters before τΛ. The present value of the amplitude F
k
(τ) = f
k
(τ)/a(τ) will be adiabatically suppressed since, as repeatedly stressed, in this regime f
k
(τ) will simply be plane waves. Consequently, defining as  the amplitude at k* = H*a* when the given mode crosses the Hubble radius, we will also have that
the amplitude at k* = H*a* when the given mode crosses the Hubble radius, we will also have that

where the subscripts (in the first equality) denote the time range over which the corresponding redshift is computed, i.e. either matter-dominated or Λ-dominated stages. The second equality follows from the first one by appreciating that a(k*) ≃  ≃ k-2 and by using Eq. (6.62). Equation (6.65) implies, immediately, that the spectral energy density of relic gravitons is corrected in two different fashions. For ν <νH the frequency dependence will be different and will be proportional to ΩGW(ν, τ0) ∝
≃ k-2 and by using Eq. (6.62). Equation (6.65) implies, immediately, that the spectral energy density of relic gravitons is corrected in two different fashions. For ν <νH the frequency dependence will be different and will be proportional to ΩGW(ν, τ0) ∝  . Vice versa, in the range ν > νH the frequency dependence will be exactly the one already computed but, overall, the amplitude will be smaller by a factor (ΩM0/ΩΛ)2. The modification of the frequency dependence is only effective between 0.36 aHz and 0.26 aHz: this effect is therefore unimportant and customarily ignored (see, for instance, [138, 140]) for phenomenological purposes. On the other hand, the overall suppression going as (ΩM0/ΩΛ)2 must be taken properly into account on the same footing of other sources of suppression of the spectral energy density. There is, in principle, a third effect which may arise and it has to do with the variation of the effective number of relativistic species. Recall, indeed, that the total energy and the total entropy densities of the plasma can be written as
. Vice versa, in the range ν > νH the frequency dependence will be exactly the one already computed but, overall, the amplitude will be smaller by a factor (ΩM0/ΩΛ)2. The modification of the frequency dependence is only effective between 0.36 aHz and 0.26 aHz: this effect is therefore unimportant and customarily ignored (see, for instance, [138, 140]) for phenomenological purposes. On the other hand, the overall suppression going as (ΩM0/ΩΛ)2 must be taken properly into account on the same footing of other sources of suppression of the spectral energy density. There is, in principle, a third effect which may arise and it has to do with the variation of the effective number of relativistic species. Recall, indeed, that the total energy and the total entropy densities of the plasma can be written as

For temperatures much larger than the top quark mass, all the known species of the minimal standard model of particle interactions are in local thermal equilibrium, then g ρ = gs = 106.75. Below, T ≃ 175 GeV the various species start decoupling, the notion of thermal equilibrium is replaced by the notion of kinetic equilibrium. The time evolution of the number of relativistic degrees of freedom effectively changes the evolution of the Hubble rate. In principle if a given mode k reenters the Hubble radius at a temperature T k the spectral energy density of the relic gravitons is (kinematically) suppressed by a factor which can be estimated as (see, for instance, [140–142])

At the present time gρ0 = 3.36 and gs0 = 3.90. In general terms the effect parametrized by Eq. (6.67) will cause a frequency-dependent suppression, i.e. a further modulation of the spectral energy density ΩGW(ν, τ0). The maximal suppression one can expect can be obtained by inserting into Eq. (6.67) the largest gs and g ρ . So, in the case of the minimal standard model this would imply that the suppression (on ΩGW(ν, τ0)) will be of the order of 0.38. In popular supersymmetric extensions of the minimal standard models g ρ and g s can be as high as, approximately, 230. This will bring down the figure given above to 0.29.
All the three effects estimated in the last part of the present section (i.e. free streaming, dark energy, evolution of relativistic degrees of freedom) have common features. Both in the case of the neutrinos and in the case of the evolution of the relativistic degrees of freedom the potential impact of the effect could be more pronounced. For instance, suppose that, in the early Universe, the particle model has many more degrees of freedom and many more particles which can free stream, at some epoch. At the same time we can say that all the aforementioned effects decrease rather than increasing the spectral energy density. Taken singularly, each of the effects will decrease ΩGW by less than one order of magnitude. The net result of the combined effects will then be, roughly, a suppression of ΩGW(ν, τ0) which is of the order of 3 × 10-2 (for 10-16 Hz <ν < 10-11 Hz) and of the order of 4 × 10-2 for ν > 10-11 Hz. These figures are comparable with the possible inaccuracies stemming from the calculation of the transfer function and, therefore, this is a further motivation, to use the transfer function of the spectral energy density. Finally the late time effects reduce a quantity which is already pretty small, i.e., as computed,  (ν, τ0) ≃ 10-15 for ν ≫ νeq.
(ν, τ0) ≃ 10-15 for ν ≫ νeq.
7 B-modes induced by long wavelength gravitons
In the minimal realization of the ΛCDM scenario the scalar fluctuations of the geometry induce an E-mode polarization which has been observed and which is now subjected to closer scrutiny [3–7] The tensor modes of the geometry not only induce an E-mode polarization but also a B-mode polarization. The detected angular power spectra due to the presence of a putative (adiabatic) curvature perturbation are the temperature autocorrelation (TT angular power spectrum) the E-mode autocorrelation (EE angular power spectrum) and their cross correlation (i.e. the TE angular power spectrum). The various angular power spectra of the temperature and polarization observables have been already defined in section 2 (see, in particular, Eqs. (2.48)-(2.49) and discussions therein). Long wavelength gravitons contribute not only to the TT, EE and TE angular power spectra but also to the B-mode autocorrelations, i.e. the BB angular power spectra. The effect of long wavelength gravitons on the temperature and polarization observables can be studied by deriving the evolution equations of the brightness perturbations which are related, in loose terms, to the fluctuations of the Stokes parameters. The tensor nature of the fluctuation defined in Eq. (2.8) plays, in this respect, a decisive role. In particular the following two points should be borne in mind:
-
in the case of the scalar modes of the geometry the heat transfer equations have an azimuthal symmetry;
-
in the case of the tensor modes the fluctuations of the brightness do depend, both, upon μ = cos ϑ as well as upon φ ; this is ultimately, the rationale for the existence of a B-mode polarization.
The heat transfer equations can be schematically written as

where  is the differential optical depth. In the differential optical depth enters not only the cross section but also the electron concentration
is the differential optical depth. In the differential optical depth enters not only the cross section but also the electron concentration  and the ionization fraction xe. The notation for the differential optical depth varies: some authors prefer κ' some other
and the ionization fraction xe. The notation for the differential optical depth varies: some authors prefer κ' some other  . Given the notations used for the conformal time coordinate we will stick to the choice made in Eq. (7.1).
. Given the notations used for the conformal time coordinate we will stick to the choice made in Eq. (7.1).
In the expression for the differential optical depth  where r0 = e2/me is the classical radius of the electron. The (differential) cross section for Compton scattering of polarized photons can be written in terms of σT and it takes the usual Klein-Nishina form:
where r0 = e2/me is the classical radius of the electron. The (differential) cross section for Compton scattering of polarized photons can be written in terms of σT and it takes the usual Klein-Nishina form:

where  and
and  are, respectively, the outgoing and ingoing polarizations of the photons; Ef and Ei are, respectively, the energies of the outgoing and of the ingoing photons. In the limit Ef ≃ Ei the differential cross section becomes, as anticipated
are, respectively, the outgoing and ingoing polarizations of the photons; Ef and Ei are, respectively, the energies of the outgoing and of the ingoing photons. In the limit Ef ≃ Ei the differential cross section becomes, as anticipated

The right left side of Eq. (7.1) constitutes the collisionless term while the right hand side is the collisional contribution. At the right-hand side of Eq. (7.3) ℳ(Ω, Ω') is, in general, a matrix whose dimensionality depends upon the specific problem. As it will be shown ℳ(Ω, Ω') can be easily computed from Eq. (7.3). In similar terms f(Ω) should be understood as a column matrix whose components are the various Stokes parameters.
7.1 Collisionless Boltzmann equation for the tensor modes
The collisionless part of the Boltzmann equation can be written as:

where qiis the comoving three-momentum of the photon. If the tensor fluctuation of the geometry is parametrized as in Eq. (2.8)

then, the right hand side of Eq. (7.4) can be written as

where the prime denotes a derivation with respect to τ and where the following identities have been used

In Eq. (7.7)  denotes the direction of the photon momentum. The third identity appearing in Eq. (7.7) stems directly from the definition of comoving three-momentum, i.e.
denotes the direction of the photon momentum. The third identity appearing in Eq. (7.7) stems directly from the definition of comoving three-momentum, i.e.

where Piis a generic spatial component of the canonical momentum obeying

Using Eq. (2.8) the full metric g ij appearing in Eq. (7.8) becomes

Consequently the comoving three-momentum qiand its conformal time derivative can be expressed as:


To obtain an explicit expression for dqi/dτ the conformal time derivative of the canonical momentum should be made explicit by using the geodesic equation, i.e.

To first order in the tensor fluctuations of the geometry the Christoffel connection will then lead to the following expression:

Using Eq. (7.14) into Eqs. (7.12) and (7.13), the third identity reported in Eq. (7.7) is quickly recovered. Depending upon the problem at hand the collisionless part of the Boltzmann equation can be written in different (but equivalent) forms. Equation (2.9) allows to write  in terms of the two polarizations:
in terms of the two polarizations:

Using Eqs. (7.7) and (7.15), Eq. (7.6) can be written, in Fourier space, as

where  denotes, for completeness, the collisional part of the Boltzmann equation;
denotes, for completeness, the collisional part of the Boltzmann equation;  is the projection of the photon momentum on the direction of the Fourier mode. If the direction of propagation of the gravitational wave coincides with the third (Cartesian) component, i.e.
is the projection of the photon momentum on the direction of the Fourier mode. If the direction of propagation of the gravitational wave coincides with the third (Cartesian) component, i.e.  . It is then easy to see that the unit vectors
. It is then easy to see that the unit vectors  and
and  must be directed, respectively, along the
must be directed, respectively, along the  and
and  Cartesian directions. This particular choice of the coordinate system implies then
Cartesian directions. This particular choice of the coordinate system implies then


Equations (7.17) and (7.18) are not symmetric for φ → -φ: while Eq. (7.17) is left unchanged, Eq. (7.18) acquires a minus sign. Conversely, the evolution equations of the scalar modes of the geometry are symmetric for φ → -φ.
7.2 Azimuthal structure of the collisional contribution
The differential cross section of Eq. (7.3) depends upon  and
and  which are, respectively, the polarizations of the outgoing and of the ingoing photons. If
which are, respectively, the polarizations of the outgoing and of the ingoing photons. If  coincides with the radial direction
coincides with the radial direction  and
and  can be written, respectively, as
can be written, respectively, as


In Eqs. (7.19) and (7.20) the components of  and
and  have been identified with the
have been identified with the  and
and  directions. This is just to guide the intuition since the components of
directions. This is just to guide the intuition since the components of  and
and  should only be orthogonal to each others and orthogonal to the direction of propagation. Furthermore notice that, in the case ϑ' = φ' = 0,
should only be orthogonal to each others and orthogonal to the direction of propagation. Furthermore notice that, in the case ϑ' = φ' = 0,

Under the transformation φ → -φ and φ' → -φ', Eqs. (7.19) and (7.20) lead to another valid choice of orthogonal frame. The intensity and the polarization of the (outgoing) radiation field will be given, respectively, as

Since Q and U are not invariant for a rotation in the polarization plane and as soon as Q is generated also U follows (see, e.g., Eqs. (2.37) and discussion therein). For pedagogical purposes, it is useful to consider, as a warm-up the simplification provided by Eq. (7.22). Consider the case where the ingoing polarization is fixed (e. g. ϑ' = φ' = 0); suppose also, for sake of simplicity, that the dependence of the Stokes parameters upon the conformal time coordinate is trivial. Using Eq. (7.3) the outgoing Stokes parameters are given by


In the generic situation the ingoing Stokes parameters do depend upon φ' and ϑ' and, therefore, the outgoing Stokes parameters are


From the definitions of  and
and  , simple trigonometric identities lead to the following expressions for the four products appearing in Eqs. (7.25) and (7.26):
, simple trigonometric identities lead to the following expressions for the four products appearing in Eqs. (7.25) and (7.26):


As already mentioned, in Eqs. (7.27) and (7.28) the notations

have been used. The results of Eqs. (7.25)-(7.26) and of Eqs. (7.27)-(7.28) allow for an explicit evaluation of the the collisional part of the Boltzmann equation which can be written, component by component, in the simplified case where f(τ, ϑ, φ) has only two components which can be identified with the intensities of the radiation field along the x and y axes

The result is:


where, by definition,




The second equality appearing in Eqs. (7.33)-(7.36) follows immediately from Eqs. (7.27) and (7.28). If  and
and  do not depend on φ', Eqs. (7.31) and (7.32) can be simplified by integrating explicitly upon φ':
do not depend on φ', Eqs. (7.31) and (7.32) can be simplified by integrating explicitly upon φ':


Equations (7.37) and (7.38) is just a useful warm-up in view of the realistic situation where:
-
the components of f(ϑ, φ) are not 2 but 3, i.e. ℐ x (ϑ, φ) and ℐ y (ϑ, φ) are supplemented by U (ϑ, φ);
-
all the 3 components of f(ϑ, φ) do depend upon φ ; in the analog of Eqs. (7.37) and (7.38) on top of the integration over μ' an integration over φ' will appear.
Since f(ϑ, φ) has now three components

ℳ(Ω, Ω'), will be a 3 × 3 matrix whose entries can be computed in full analogy with what has been already done in Eqs. (7.33)-(7.36). In general terms, the ingoing electric field can be expressed as

implying that the outgoing Stokes parameters can be written as



where, for the moment, the collisionless part of the Boltzmann equation has been neglected. Inserting Eq. (7.40) into Eqs. (7.41)-(7.43) the explicit form of ℳ(Ω, Ω') since the Stokes parameters of the ingoing radiation field are nothing but

The terms ℳ11, ℳ12, ℳ21, ℳ22 will be exactly the ones already evaluated in Eqs. (7.33)-(7.36). The remaining entries are found to be





As in Eqs. (7.33)-(7.36), the second equality in each of Eqs. (7.45)-(7.49) follows immediately from Eqs. (7.27) and (7.28). A final remark on the symmetry properties of the various entries of ℳ(Ω, Ω') is in order:
-
ℳ11, ℳ12, ℳ21, ℳ22 and ℳ33 are all symmetric under the simultaneous transformation φ → -φ and φ' → -φ';
-
for the same transformation, the remaining entries flip their respective sign.
7.3 Different parametrizations of the full equation
The phase space distribution obeying the collisionless part of the Boltzmann equation (see, e. g., Eq. (7.16)) does depend upon k = | |(i.e. the Fourier mode). In the previous subsection the dependence upon k has been suppressed (for sake of simplicity) since all the aforementioned considerations could be separately repeated for each Fourier mode. Similarly, from Eq. (7.16), it is clear that the phase-space distribution does depend not only upon
|(i.e. the Fourier mode). In the previous subsection the dependence upon k has been suppressed (for sake of simplicity) since all the aforementioned considerations could be separately repeated for each Fourier mode. Similarly, from Eq. (7.16), it is clear that the phase-space distribution does depend not only upon  (i.e. the direction of the photon) but also upon its comoving three-momentum. The phase space distribution consists of 3 independent functions whose dependence can be written, in Fourier space, as:
(i.e. the direction of the photon) but also upon its comoving three-momentum. The phase space distribution consists of 3 independent functions whose dependence can be written, in Fourier space, as:

As already discussed it is more handy to use directly μ = cosϑ as independent variable. The full Boltzmann equation can then be solved by iteration around the equilibrium configuration provided by the Bose-Einstein distribution f0(q); this means that the 3 components of f (τ, μ, φ) can be written as:



The solution of the problem will then require the determination of  (k, τ, μ, φ),
(k, τ, μ, φ),  (k, τ, μ, φ) and
(k, τ, μ, φ) and  (k, τ, μ, φ). The form of the final solution for
(k, τ, μ, φ). The form of the final solution for  (k, τ, μ, φ),
(k, τ, μ, φ),  (k, τ, μ, φ) and
(k, τ, μ, φ) and  (k, τ, μ, φ) will depend upon the polarization of the relic graviton. This aspect cal be appreciated by looking at the collisionless part of the full Boltzmann equation, i.e. Eq. (7.16). Consider, for sake of concreteness, the case of the ⊕ polarization. Inserting Eq. (7.50) into Eq. (7.16) and using the perturbative scheme of Eqs. (7.51)-(7.53), the three independent components of the Boltzmann equation become:
(k, τ, μ, φ) will depend upon the polarization of the relic graviton. This aspect cal be appreciated by looking at the collisionless part of the full Boltzmann equation, i.e. Eq. (7.16). Consider, for sake of concreteness, the case of the ⊕ polarization. Inserting Eq. (7.50) into Eq. (7.16) and using the perturbative scheme of Eqs. (7.51)-(7.53), the three independent components of the Boltzmann equation become:



where, for convenience, the collision terms  (k, τ, μ, φ),
(k, τ, μ, φ),  (k, τ, μ, φ) and
(k, τ, μ, φ) and  (k, τ, μ, φ) have been expressed as:
(k, τ, μ, φ) have been expressed as:



In the case of the ⊗ polarization Eqs. (7.54)-(7.56) lead to a similar result where, however, the relevant part of the collisionless contribution is different and it is given by the replacement

as it can be argued directly from Eq. (7.16). By inspecting Eqs. (7.54), (7.55) and (7.56) it is possible to argue that the azimuthal structure of the equations, appearing in connection with the polarization of the gravitational wave, can be decoupled from the radial structure by appropriately writing the various Stokes parameters. In the case of the ⊕ polarization, symmetry considerations demand that a sound ansatz for the full solution can be written in terms of two independent functions, i.e. β (k, τ, μ, φ) and ζ (k, τ, μ, φ):



In the case of the ⊗ polarization the azimuthal structure of the collisionless Boltzmann equation changes because of the replacement of Eq. (7.60). The analog of Eqs. (7.61)-(7.63) become, in the case of the ⊗ polarization,



Using, alternatively, either Eqs. (7.61)-(7.63) or Eqs. (7.64)-(7.66) the explicit evolution equations obeyed by β (k, τ, μ, φ) and ζ (k, τ, μ, φ) can be derived. For sake of concreteness consider again the case of the ⊕ polarization and insert Eqs. (7.61), (7.62) and (7.63) into Eqs. (7.57), (7.58) and (7.59). In the collision terms the integrations over φ' can be performed by recalling that



Consequently, Eqs. (7.57), (7.58) and (7.59) become



Now the essential steps of the derivation are the following:
-
Eqs. (7.61)-(7.63) must be inserted, respectively, at left hand side of Eqs. (7.54)-(7.56);
-
Eqs. (7.70)-(7.72) must be inserted, respectively, at the right hand side of Eqs. (7.54)-(7.56).
The final result of the previous pair of manipulations can be explicitly written as



where Ψ (k, τ) is given by

As in the previous sections the  and
and  denote the time derivatives of the polarizations with respect to the conformal time coordinate τ. This notation has been avoided in the previous equations of the present section since it could have been confused with the angular variables describing the polarizations of the outgoing photons. From now on this possible clash of notations does not arise.
denote the time derivatives of the polarizations with respect to the conformal time coordinate τ. This notation has been avoided in the previous equations of the present section since it could have been confused with the angular variables describing the polarizations of the outgoing photons. From now on this possible clash of notations does not arise.
As expected, one of the three equations appearing in Eqs. (7.73)-(7.74) is redundant. Inserting Eq. (7.75) into Eq. (7.74) the two independent equations turn out to be


Concerning the result obtained in Eqs. (7.77) and (7.78) few comments are in order:
-
in Eqs. (7.77)-(7.78)
 denotes indifferently either
denotes indifferently either  or
or  : the derivation reported in the case of h⊕ can be repeated in the case of h⊗ bearing in mind the differences in the angular structure (i.e. Eqs. (7.64)-(7.66) should be used instead of Eqs. (7.61)-(7.63));
: the derivation reported in the case of h⊕ can be repeated in the case of h⊗ bearing in mind the differences in the angular structure (i.e. Eqs. (7.64)-(7.66) should be used instead of Eqs. (7.61)-(7.63)); -
by changing φ → -φ and φ' → -φ', Eqs. (7.61)-(7.63) and Eqs. (7.64)-(7.66) will be different because if the various sines appearing the various expressions; therefore the angular structure of the Stokes parameters will change but Eqs. (7.77) and (7.78) will keep their form.
The rationale for the latter statement is that while φ → -φ and φ' → -φ' changes the angular structure of the Stokes parameters, also some of the entries of ℳ(Ω, Ω') will change. The net result, as already mentioned, will be that Eqs. (7.77) and (7.78) will still be valid. The result expressed by Eqs. (7.77) and (7.78) has been firstly obtained by Polnarev [143] and then exploited for different semi-analytical discussions of the problem (see, e. g. [144–146]). The polarization decomposition leading to Eqs. (7.77) and (7.78) can be related to slightly different treatments (see, for instance, [98]) using the brightness perturbations rather than β and ζ. The connection between the different formalisms will be explored later in this section. By summing up Eqs. (7.77) and (7.78) the collision terms cancel:

Defining ξ = β + ζ the collision term of Eq. (7.76) can also be written as:

The collision term can be further simplified by expanding in multipoles the unknowns β (k, μ, τ) and ζ (k, μ, τ)

where Pℓ(μ) denote, as usual, the Legendre polynomials. By recalling that the first three Legendre polynomials of even order are

the orthogonality of the Legendre polynomials imply that the integral over x in Eq. (7.80) leads to

So far the discussion has been conducted in terms of one single polarization at the time. For both polarizations the evolution equations of ζ and β turn out to be, of course, the same. However the azimuthal structure of the relevant Stokes parameters will be different for different poolarizations. In view of specific applications it is useful to introduce a unified notations allowing for the simultaneous treatment of the two different cases:



where, following Eqs. (5.11)-(5.13) (see also [98]) the stochastic variables

have been introduced. Note that, Eqs. (7.85) and (7.86) reproduce exactly Eqs. (7.61)(7.63) (when e⊗ ( ) = 0). Similarly, when e⊕(
) = 0). Similarly, when e⊕( ) = 0, Eqs. (7.64)-(7.66) are correctly recovered. The variables of Eq. (7.87) assume (see also Eqs. (5.12)-(5.13)) that the time dependence can be factorized by in terms of an appropriate transfer function for the amplitude. By linearly combining Eqs. (7.85) and (7.86) it is also easy to obtain
) = 0, Eqs. (7.64)-(7.66) are correctly recovered. The variables of Eq. (7.87) assume (see also Eqs. (5.12)-(5.13)) that the time dependence can be factorized by in terms of an appropriate transfer function for the amplitude. By linearly combining Eqs. (7.85) and (7.86) it is also easy to obtain


The dependence of Eqs. (7.78) and (7.79) on the derivative of f0(q) with respect to the comoving three-momentum q can be further simplified by rephrasing the Boltzmann equations in terms of the appropriate brightness perturbations. Recalling that, by definition of brightness perturbations,

the intensity  introduced in Eq. (7.84) can be written as ⊠ = -ΔI(∂ ln f0/∂ ln q). Consequently, Eqs. (7.84) and (7.88)-(7.89) can also be written as:
introduced in Eq. (7.84) can be written as ⊠ = -ΔI(∂ ln f0/∂ ln q). Consequently, Eqs. (7.84) and (7.88)-(7.89) can also be written as:



where the relation of ΔT(k, τ, μ) and ΔP(k, τ, μ) to β (k, τ, μ) and ζ (k, τ, μ) is

Using Eq. (7.94) inside Eqs. (7.78)-(7.79), the evolution equations obeyed by ΔP(k, τ, μ) and ΔT(k, τ, μ) can be obtained and it is:



In Eq. (7.96) h is the canonical amplitude of the graviton. Recalling the results of section 3 it has been defined that h⊕ =  ℓP h and h⊗ =
ℓP h and h⊗ =  ℓP h. The
ℓP h. The  factor simplifies once the brightness perturbations of Eqs. (7.94) are used. Using the common practice Eqs. (7.95)-(7.97) have been written in units ℓP = 1.
factor simplifies once the brightness perturbations of Eqs. (7.94) are used. Using the common practice Eqs. (7.95)-(7.97) have been written in units ℓP = 1.
After Eqs. (7.19) and (7.20) it has been stressed that by flipping the sign of φ and φ' the outgoing and ingoing polarizations change but the choice of orthnormal frame is still valid. The discussion conducted so far can be repeated by assuming the polarizations of Eqs. (7.19) and (7.20) but with φ → -φ and φ' → -φ'. The same sign flip can be followed throughout the derivation and it can be appreciated that the results of Eqs. (7.95), (7.96) and (7.97) are left unchanged (see also discussion after Eqs. (7.48)-(7.49)). The flip in the sign of φ and φ' affects, however, the brightness perturbations. The intensity of the radiation field, as expected, is left invariant when φ → -φ (see Eq. (7.91)). On the contrary, by repeating all the steps of the derivation, Eqs. (7.92) and (7.93) are modiffed. Consequently, by flipping the sign of φ, Eqs. (7.91), (7.92) and (7.93) become



In [98] the brightness perturbations for the poolarization have been assigned as in Eqs. (7.99)-(7.100) and not as Eqs. (7.92) and (7.93). The ladder operators of Eqs. (2.52) and (2.53) are not invariant under the transformation φ → -φ. More specifically the spin weight of a given function changes the sign whenever φ → -φ. Equations (2.52) and (2.53) are consistent with the brightness perturbations written as in Eqs. (7.99) and (7.100). To be consistent with the customary notations we will therefore adhere to the conventions stipulated in [98].
7.4 B-modes from relic gravitons
The analytic and numerical solutions of the evolution equations for the brightness perturbations allow for an explicit evaluation of the temperature and polarization observables. The results obtained so far imply that long wavelength gravitons will produce both temperature and polarization anisotropies. More specifically, following the terminology of section 2 (see, in particular, Eqs. (2.48)-(2.50)) the relevant angular power spectra induced by the relic gravitons will be the TT, EE, TE and BB angular power spectra.
The explicit form of  and
and 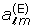 can be derived from the general expressions already encountered, respectively, in Eqs. (2.72) and (2.73). The integrands of Eqs. (2.72) and (2.73) can be computed from the action of the the differential operators of Eqs. (2.52)-(2.53), i.e., more specifically,
can be derived from the general expressions already encountered, respectively, in Eqs. (2.72) and (2.73). The integrands of Eqs. (2.72) and (2.73) can be computed from the action of the the differential operators of Eqs. (2.52)-(2.53), i.e., more specifically,


Equations (2.72) and (2.73) become then


In Eqs. (7.103)-(7.104) the prime denotes a derivation with respect to μ = cosϑ. This notation will be consistently followed, for sake of simplicity, but only in this subsection. Equations (7.103) and (7.104) can be easily written in even more explicit terms and, as before, it is easier to focus on a single polarization, e. g. ⊕:

Inserting Eq. (7.105) into Eqs. (7.103) and (7.104) the resulting expressions will be


In Eqs. (7.106) and (7.107) the explicit integration over the angular variables can be performed in explicit terms. Consider, in particular, Eq. (7.106), i.e.

Bearing in mind the connection between spherical harmonics and the associated Legendre functions, the Yℓm( ) will be essentially given by the product of
) will be essentially given by the product of  (μ) and of eimφ, up to a well know normalization coefficient. In Eq. (7.108) the integration over φ can be carried on in explicit terms and since there is a sin 2φ in the integrand the whole integral will be proportional to (δm, 2 - δm-2); in more precise terms the integration over φ will bring Eq. (7.108) in the form:
(μ) and of eimφ, up to a well know normalization coefficient. In Eq. (7.108) the integration over φ can be carried on in explicit terms and since there is a sin 2φ in the integrand the whole integral will be proportional to (δm, 2 - δm-2); in more precise terms the integration over φ will bring Eq. (7.108) in the form:

Equation (7.109) can be further simplified by using the following three relations:



Equations (7.111) and (7.112) are well known recurrence relations for the for the associated Legendre functions (see p. 24 of Ref. [93] for a derivation). Equation (7.110) can be written in slightly different ways. Some authors do not include, at the right hand side of Eq. (7.110), the factor (-i)jinside the sum (see for instance [100]). The analog of Eq. (7.109) can also be obtained within the approach of Ref. [100] whose conventions (for the ⊕ polarization) are

with

For × polarization, the angular structure of Eq. (7.114) will be different and can be obtained from the results for the ⊕ polarization by replacing cos 2φ → sin 2φ and sin 2φ → - cos 2φ. Eqs. (7.113) and (7.114) are nothing but the explicit expression of the polarization tensor on the sphere introduced in Eq. (2.81) with the difference that the indices (in Eq. (2.81)) are both covariant while in Eq. (7.113) they are both contravariant. The conventions of [100] imply also a difference of a factor of 1/8 in comparison with the conventions adopted here. Equations (7.111) and (7.112) can be used inside Eq. (7.109). As an example the term (1 - μ2)μ  , after using Eq. (7.110) will produce a factor μ (1 - μ2)
, after using Eq. (7.110) will produce a factor μ (1 - μ2) , i.e.
, i.e.

where the first equality follows from the definition of the associated Legendre functions (i.e. Eq. (2.55)) while the second follows from Eq. (7.111) with m = ± 2. The second term in the integrand of Eq. (7.109), i.e. (1 - μ2)  will produce a factor (1 - μ2)
will produce a factor (1 - μ2)  , i.e.
, i.e.

where, again, the first and second equalities follow, respectively, from Eqs. (2.55) and Eq. (7.111) both in the case m = ± 2. Inserting Eqs. (7.115) and (7.116) inside Eq. (7.109) the integration over μ can be performed by simply using the orthogonality of the associated Legendre functions, i.e.

The final result for the B-mode will then be:

If the factor (-i)jwould be absent from the expansion of Eq. (7.110) there would not be (-i)ℓ at the right-hand side of Eq. (7.118); for the same reason, the relative sign of the two terms inside the squared bracket would be plus instead of minus. Finally, the factor (1/8) appearing at the right-hand side of Eq. (7.113) will also modify slightly the prefactor of Eq. (7.118) which will be

where Eq. (2.102) has been used to relate  and
and  . In the case of the E-mode, always working with the ⊕ polarization, Eqs. (7.104) and (7.107) will give, after integration over φ,
. In the case of the E-mode, always working with the ⊕ polarization, Eqs. (7.104) and (7.107) will give, after integration over φ,

where Eqs. (2.54) and (2.55) have been used. To complete the calculation it is necessary to perform the integration over μ. This can be done, as previously shown, by using wisely the recursion relations of the associate Legendre functions. From Eq. (7.120) we have that, using the expansion of Eq. (7.110),

As in the case of the B-mode, the main idea of the calculation is to express the relevant part of the integrand appearing at the right hand side of Eq. (7.121) in terms of products of associated Legendre functions with the same m but different values of j so that the orthogonality relation (7.117) can be exploited. Using the definition of the associated Legendre functions of Eq. (2.55) it is easy to show that

where the minus sign in the second term at the right hand side of Eq. (7.122) arises since the Condon-Shortley phase has been included in the definition of the associated Legendre functions (see Eqs. (2.54)-(2.55) and discussion therein). The right hand side of Eq. (7.122) now be simplified by using the following steps:
-
Eq. (7.111) can be used to simplify the term
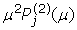 ;
; -
Eq. (7.112) can be used to simplify the term
 ;
; -
the term (1 - μ2)Pj(μ) can be simplified by using the equation of the Legendre polynomials and the recursion relations (7.111) and (7.112).
Using these three steps, a rather lengthy but straightforward algebra leads to the following expression:

To get to Eq. (7.123) it is useful to recall, on a side, that

which can be derived by recalling the equation obeyed by the Legendre polynomials P j (μ) as well as the recursion relations reported in Eqs. (7.111)-(7.112). Using Eq. (7.124) inside Eqs. (7.120)-(7.121) it is easy to obtain, after simple algebra, that

As in the case of the B-mode the presence of the factor (-i)jin Eq. (7.110) leads to a sign difference in the terms ΔP ℓ ± 2 appearing in Eq. (7.125). The absolute values of the coefficients of the three terms appearing (inside the the square bracket) in Eq. (7.125) are independent on the conventions related to Eq. (7.110). The coefficient of the term ΔP ℓ appears to be different from the homologue term reported in Eq. (4.41) of [100]. After many checks and cross-checks of the derivations leading to Eq. (7.125) it has been concluded that the difference (i.e. 6ℓ(ℓ + 1) instead of 6(ℓ - 1)(ℓ + 2) in the numerator of the coefficient of ΔP ℓ) is just the result of a typo and the correct expression is 6(ℓ - 1)(ℓ + 2) as in Eq. (7.125).
7.5 Angular power spectra induced by long wavelength gravitons
The tensor modes of the geometry produce both, temperature and polarization anisotropies. Consider, for simplicity, the ΛCDM parameters determined from the best fit of the WMAP 5-yr data alone. These parameters have been reported in Eq. (2.7). In Fig. 10 the TT angular power spectra stemming from the standard adiabatic mode and the temperature autocorrelations induced by the tensor modes are illustrated.
In both plots of Fig. 10 the full line denotes the TT angular power spectra corresponding to the best fit of the WMAP 5-yr data alone. In the plot at the left the dashed and dot-dashed lines illustrate, respectively, the cases rT = 0.1 and rT = 0.2. The tensor spectral index is fixed according to Eqs. (1.2) and (1.6) (see also Eqs. (6.4) and (6.5)). In both plots of Fig. 10 the spectral index does not run, i.e. αT = 0 in Eq. (1.6). Always in Fig. 10 (plot at the right) the dashed line denotes the tensor contribution in the case rT = 1 while the dot-dashed line denotes the total TT angular power spectrum. The temperature and polarization observables can be obtained numerically (see, e.g. [98, 100]) but useful analytic results do exist in the literature [143–146, 140]. The numerical code used for the calculation of the plots reported in Fig. 10 (as well as in the following figures of the present section, i.e. Figs. 11 and 12) is a modiffed version of the program described in [98, 100] (i.e. CMBFAST). An essential step for both analytic and numerical approaches is to derive the angular power spectra in more explicit terms and as a function of the solution of the heat transfer equations. The solution of Eqs. (7.95), (7.96) and (7.97) can be formally written by using the integration along the line of sight which is also common to the scalar case (see, e.g. [127], for an introduction):


where x = k(τ0 -τ). Note that ST(k, τ) and SP(k, τ) are related to the source terms of, respectively, Eqs. (7.95) and (7.96), i.e.

where S(k, τ) is given by Eq. (7.97) and where

is the visibility function expressed in terms of the differential optical depth ϵ' and in terms of the optical depth ϵ(τ, τ0). The visibility function  (τ) gives that probability that a photon is last scattered between τ and τ + dτ. In loose terms the visibility function is peaked around the redshift of recombination. In analytic discussions the visibility function is often approximated by means of a Gaussian profile (see, e. g., [128, 140, 127] and also [147–150]):
(τ) gives that probability that a photon is last scattered between τ and τ + dτ. In loose terms the visibility function is peaked around the redshift of recombination. In analytic discussions the visibility function is often approximated by means of a Gaussian profile (see, e. g., [128, 140, 127] and also [147–150]):

As indicated in Eq. (7.130),  (σrec) is determined by requiring that the integral of
(σrec) is determined by requiring that the integral of  (τ) over τ is normalized to 1. The WMAP data suggest a thickness (in redshift space) Δzrec ≃ 195 ± 2 [8] which would imply that σrec, in units of the (comoving) angular diameter distance to recombination, can be estimated as σrec/τ0 ≃ 1.43 × 10-3. When τ0 ≫ τrec and τ0 ≫ σrec the normalization appearing in Eq. (7.130) can be estimated as
(τ) over τ is normalized to 1. The WMAP data suggest a thickness (in redshift space) Δzrec ≃ 195 ± 2 [8] which would imply that σrec, in units of the (comoving) angular diameter distance to recombination, can be estimated as σrec/τ0 ≃ 1.43 × 10-3. When τ0 ≫ τrec and τ0 ≫ σrec the normalization appearing in Eq. (7.130) can be estimated as  . In [140] it has been suggested that a better approximation, for the case of the tensor modes, is to assume that
. In [140] it has been suggested that a better approximation, for the case of the tensor modes, is to assume that  (τ) has two different widths, respectively, for τ <τrec and for τ > τrec. Recalling now Eq. (2.44) and (2.49) the
(τ) has two different widths, respectively, for τ <τrec and for τ > τrec. Recalling now Eq. (2.44) and (2.49) the  can be written as
can be written as

where the second equality follows from the Fourier transform of ΔI( ) and by using Eq. (7.98) in the obtained expression. The angular integrations can now be performed with the approach already exploited in previous subsection for the polarization observables. It is however useful to solve Eq. (7.131) with a slightly different method (see, e. g. [98]) where explicit use is made of the solutions (7.126) and (7.127).
) and by using Eq. (7.98) in the obtained expression. The angular integrations can now be performed with the approach already exploited in previous subsection for the polarization observables. It is however useful to solve Eq. (7.131) with a slightly different method (see, e. g. [98]) where explicit use is made of the solutions (7.126) and (7.127).
Indeed, inserting Eq. (7.126) into Eq. (7.131)  can be written as
can be written as


In  the integration over φ is trivial since the (ordinary) spherical harmonics depend upon φ as eim φ(see, e. g., Eqs. (2.54) and (2.55)). Thus, as expected on the basis of the results of the previous subsection,
the integration over φ is trivial since the (ordinary) spherical harmonics depend upon φ as eim φ(see, e. g., Eqs. (2.54) and (2.55)). Thus, as expected on the basis of the results of the previous subsection,  ∝ 2π δm, ±2. The latter results allows for a simplification so that, for instance,
∝ 2π δm, ±2. The latter results allows for a simplification so that, for instance,

where the second equality follows by first integrating by parts and by then expanding e-iμxin series of Legendre polynomials. Indeed, in Eq. (7.134), jℓ(x) are the spherical Bessel functions. Note, finally that, inside the integral of Eq. (7.134) expressions like (1 - μ2)2e-iμxcan be traded for  . Recalling the properties of the associated Legendre (see second relation of Eq. (2.55)) the other integral, i.e.
. Recalling the properties of the associated Legendre (see second relation of Eq. (2.55)) the other integral, i.e.  (ℓ, m, x) can be performed exactly in the same way. By making explicit the ensemble averages and by using Eq. (2.49), the angular power spectrum illustrated in Fig. 10 can be obtained and it is given by:
(ℓ, m, x) can be performed exactly in the same way. By making explicit the ensemble averages and by using Eq. (2.49), the angular power spectrum illustrated in Fig. 10 can be obtained and it is given by:

where, as in Eq. (2.46),  . Having discussed the temperature autocorrelation induced by the long wavelength gravitons it is now the moment of discussing the polarization observables. In Fig. 11 (plot at the left) the EE angular power spectra (full line) are compared with the B-mode autocorrelations (dashed line) induced by the tensor modes in the case rT = 0.1 while the other cosmological parameters are fixed to the best-fit values of the WMAp 5-yr data alone. Always in Fig. 11 (plot at the right) the full line illustrates the B-mode autocorrelation in the case rT = 0.1 while the dashed line illustrated the EE angular power spectrum stemming from the standard adiabatic mode. In Fig. 12 (plot at the left) the BB angular power spectra are illustrated for different values of rT compatible with current bounds on rT (see Tabs. 1 and 2).
. Having discussed the temperature autocorrelation induced by the long wavelength gravitons it is now the moment of discussing the polarization observables. In Fig. 11 (plot at the left) the EE angular power spectra (full line) are compared with the B-mode autocorrelations (dashed line) induced by the tensor modes in the case rT = 0.1 while the other cosmological parameters are fixed to the best-fit values of the WMAp 5-yr data alone. Always in Fig. 11 (plot at the right) the full line illustrates the B-mode autocorrelation in the case rT = 0.1 while the dashed line illustrated the EE angular power spectrum stemming from the standard adiabatic mode. In Fig. 12 (plot at the left) the BB angular power spectra are illustrated for different values of rT compatible with current bounds on rT (see Tabs. 1 and 2).
The E-mode and the B-mode angular power spectra can be obtained from Eqs. (7.99) and (7.100) by carefully following all the steps leading to the temperature autocorrelation of Eq. (7.135). The crucial difference will be, of course, that 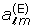 and
and  arise, respectively, in the expansion of ΔE(
arise, respectively, in the expansion of ΔE( ) and ΔB(
) and ΔB( ) as reported in Eq. (2.46). To compute
) as reported in Eq. (2.46). To compute 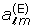 and
and  in terms of SP(k, τ) the steps are, in short, the following:
in terms of SP(k, τ) the steps are, in short, the following:
-
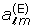 and
and  should be first expressed in terms of ΔE(
should be first expressed in terms of ΔE( ) and ΔB(
) and ΔB( ) as in Eq. (2.46);
) as in Eq. (2.46); -
then Eqs. (7.99) and (7.100) should be inserted into Eqs. (2.65) and (2.66);
-
the evolution for ΔP(k, μ, τ) can then be solved in Fourier space as in Eq. (7.126).
The first and the second step has been already (partially) performed in the previous subsection and the results have been given in Eqs. (7.103)-(7.104) with the difference that, now, the two polarizations can be treated simultaneously so that, in Fourier space,


Note that Eqs. (7.136) and (7.137) follow directly from Eqs. (7.99) and (7.100) by definition of Δ± ( , τ, μ, φ). It should be appreciated that one derivation with respect to φ changes the azimuthal structure of ΔQ(
, τ, μ, φ). It should be appreciated that one derivation with respect to φ changes the azimuthal structure of ΔQ( , τ, μ, φ) and ΔU(
, τ, μ, φ) and ΔU( , τ, μ, φ), i.e.
, τ, μ, φ), i.e.


Using now Eqs. (7.136)-(7.137) and (7.138)-(7.139) inside Eqs. (7.103) and (7.104) we do get, after Fourier transform,


According to Eq. (7.126) ΔP(k, μ, τ0) can be related to SP(k, τ) and the resulting coefficients are:


where  (x) and
(x) and  (x) are two differential operators, i.e.
(x) are two differential operators, i.e.

Now Eqs. (7.142) and (7.143) can be used into Eqs. (2.48) and the angular power spectra become:


where


The tensor modes also induce a TE angular power spectrum (i.e. a cross-correlation between the temperature and the E-mode polarization). In Fig. 12 (plot at the right) the absolute value of the TE (tensor) angular power spectrum is compared with the corresponding angular power spectrum induced by the standard adiabatic mode. The cross-correlation between temperature and polarization can be obtained inserting Eqs. (7.133) and (7.141) into Eq. (2.49) and the result is

where, ΔTℓ(k, τ0) and ΔEℓ(k, τ0) are given, respectively, by Eqs. (7.135) and (7.147). It should finally be mentioned that the derivatives with respect to x appearing in Eqs. (7.147) and (7.148) can be transformed into derivatives with respect to τ by making use of integration by parts [98]. This step is carried on in full analogy with what happens with the scalar modes of the geometry [127].
Various experiments provided, so far, direct limits on the B-mode polarization.
The limits on rT reported in Tabs. 1 and 2 follow from a combined analysis of the TT, EE and TE angular power spectra which allows for a tensor contribution. As Tab. 3 indicates the upper limits on the B-mode polarization are still rather loose and, often, derived on the basis of a limited range of harmonics. The harmonics probed by the different experiments listed in Tab. 3 are also illustrated in Fig. 13. It is clear from Fig. 13 that the present measurements are consistent with zero and that, therefore, the results must be correctly interpreted as upper limits on the B-mode polarization.
8 High-frequency spikes in the relic graviton background
In the ΛCDM paradigm long wavelength gravitons can affect the CMB polarization. As the frequency increases towards the region accessible to wide band interferometers, the ΛCDM signal can only decrease for number of independent reasons:
-
in the ΛCDM paradigm the spectral energy density is only approximately scale-invariant (see, e.g. Fig. 2) but the scaling violations always tend to make the spectral energy density smaller at high frequencies;
-
there are various secondary effects associated, for instance, with the variation of the effective number of relativistic degrees of freedom, with the neutrino anisotropic stress and with the transition to a phase dominated by the dark-energy contribution: all these features reduce the spectral energy density in different frequency regions;
-
the addition of supplementary scalar fields driving the inflationary phase does not change the two previous statements.
The previous conclusions are all based (either directly or indirectly) on the assumption that the thermal history of the Universe is minimal in the sense that, after inflation, the Universe soon becomes dominated by relativistic particles so that the sound speed of the plasma soon reaches values cst = 1/ . The post-inflationary thermal history might not be minimal. For instance it could happen that the transition to the radiation-dominated regime is not instantaneous [82]. More specifically it can happen that, after inflation, the sound speed of the plasma is such that cst > 1/
. The post-inflationary thermal history might not be minimal. For instance it could happen that the transition to the radiation-dominated regime is not instantaneous [82]. More specifically it can happen that, after inflation, the sound speed of the plasma is such that cst > 1/ . When the sound p speed is larger than 1/
. When the sound p speed is larger than 1/ , the fluid is said to be stiff. In the system of units used in the present paper the speed of light is such that c = 1. A natural upper limit for the sound speed is exactly 1 which is the maximally stiff fluid compatible with causality [132] (see, however, also [133]). If the thermal history of the Universe contemplates a post-inflationary phase stiffer than radiation, a spike in the relic graviton spectrum is expected at high frequencies [82] (see also [83, 84] as well as Eqs. (6.29)-(6.30) and discussion therein). The possibility of having a post-inflationary phase stiffer than radiation has been also investigated in different contexts such as in [151–153].
, the fluid is said to be stiff. In the system of units used in the present paper the speed of light is such that c = 1. A natural upper limit for the sound speed is exactly 1 which is the maximally stiff fluid compatible with causality [132] (see, however, also [133]). If the thermal history of the Universe contemplates a post-inflationary phase stiffer than radiation, a spike in the relic graviton spectrum is expected at high frequencies [82] (see also [83, 84] as well as Eqs. (6.29)-(6.30) and discussion therein). The possibility of having a post-inflationary phase stiffer than radiation has been also investigated in different contexts such as in [151–153].
In the early Universe, the dominant energy condition might be violated and this observation will also produce scaling violations in the spectral energy density [154, 155]. If we assume the validity of the ΛCDM paradigm, a violation of the dominant energy condition implies that, during an early stage of the life of the Universe, the effective enthalpy density of the sources driving the geometry was negative and this may happen in the presence of bulk viscous stresses [154, 155] (see also [156, 157] for interesting reprises of this idea). In what follows the focus will be on the more mundane possibility that the thermal history of the plasma includes a phase where the speed of sound was close to the speed of light.
Absent any indirect tests on the thermal history of the Universe prior to the formation of light nuclear elements, it is legitimate to investigate situations where, before nucleosyntheis, the sound speed of the plasma was larger than 1/ , at most equalling the speed of light. In this plausible extension of the current cosmological paradigm, hereby dubbed Tensor-ΛCDM (i.e. TΛCDM) scenario, high-frequency gravitons are copiously produced [46, 47]. Without conflicting with the bounds on the tensor to scalar ratio stemming from the combined analysis of the three standard cosmological data sets (i.e. cosmic microwave background anisotropies, large-scale structure data and observations of type Ia supenovae), the spectral energy density of the relic gravitons in the TΛCDM scenario can be potentially observable by wide-band interferometers (in their advanced version) operating in a frequency window which ranges between few Hz and few kHz.
, at most equalling the speed of light. In this plausible extension of the current cosmological paradigm, hereby dubbed Tensor-ΛCDM (i.e. TΛCDM) scenario, high-frequency gravitons are copiously produced [46, 47]. Without conflicting with the bounds on the tensor to scalar ratio stemming from the combined analysis of the three standard cosmological data sets (i.e. cosmic microwave background anisotropies, large-scale structure data and observations of type Ia supenovae), the spectral energy density of the relic gravitons in the TΛCDM scenario can be potentially observable by wide-band interferometers (in their advanced version) operating in a frequency window which ranges between few Hz and few kHz.
The presence of a stiff phase increases the spectral energy density for frequencies larger than a pivotal frequency νs which is related to the total duration of the stiff phase. If the stiff phase takes place before BBN, then νs > 10-2 nHz. If the stiff phase takes place for equivalent temperatures larger than 100 GeV, then νs ≥ μHz. If the stiff phase takes place for T ≥ 100 TeV, then νs > mHz. The frequency νs marks the beginning of a branch of the spectrum where the tilt of the spectral energy density is blue (i.e. increasing in slope) rather than nearly scale invariant or slightly red (as it is the case in the conventional scenario).
8.1 Scaling violations
In the ΛCDM paradigm, for frequencies larger than νeq the spectral energy density of the relic gravitons is, approximately, scale invariant (see Fig. 2). In the context of the TΛCDM scenario the approximate scale-invariance of the at plateau is violated. This situation is illustrated, for instance, in Fig. 4. In the present subsection a more detailed account of the typical frequencies of the problem will be presented. If there is some delay between the end of inflation and the onset of radiation the maximal wavenumber of the spectrum will be given by:

where α = 2/[3(wt + 1)] (with wt > 1/3) is related to the specific kind of stiff dynamics. Equation (8.1) can also be written as

where

In the case Σ =  (1) (as it happens in the case α = 1/3 if the initial radiation is in the form of quantum fluctuations) νmax = kmax/(2π) ≃ 100 GHz, more precisely:
(1) (as it happens in the case α = 1/3 if the initial radiation is in the form of quantum fluctuations) νmax = kmax/(2π) ≃ 100 GHz, more precisely:

On top of the standard parameters of the ΛCDM scenario (see, e. g., Eq. (2.7)) the minimal TΛCDM scenario demands two supplementary parameters
-
the frequency νs defining the region of the spectrum at which the scaling violations take place;
-
the slope of the spectrum arising during the stiff phase.
The frequency νs can be dynamically related to the frequency of the maximum and, consequently, the first parameter can be trated for Σ. As it will be shown in a moment, typical values for Σ range between 0.01 and 0.5. The slope of the spectrum during the stiff phase depends upon the total barotropic index and can therefore be traded for wt. The curvature scale Hr determines ks (or νs), i.e. the frequency at which the spectral energy density starts increasing. Supposing that from the end of inflation there is a single stiff phase (as it is natural to assume in a minimalistic persepective) the value of ks is

Using the relation of Hr to Σ, Eq. (8.5) can also be written as

and as

The quantity Σ which parametrizes the location, in the spectrum, where the scaling violations appear must be smaller than 1 or, at most, of order 1. This is what happens within specific models. For instance, if the radiation present at the end of inflation comes from amplified quantum fluctuations (i.e. Gibbons-Hawking radiation), quite generically, at the end of inflation ρr ≃ H4. More specifically

In Eq. (8.8) Neff is the number of species contributing to the quantum fluctuations during the quasi-de Sitter stage of expansion. In [135] (see also [83–85]) it has been argued that this quantity could be evaluated using a perturbative expansion valid in the limit of quasi-conformal coupling. It should be clear that Neff is conceptually different from the number of relativistic degrees of freedom g ρ . Given H and Neff the length of the stiff phase is fixed, in this case, by [85]

where we used the fact that α = 2/[3(w + 1)] and where we defined λ = Neff/(480π2). Equation (8.9) implies that

Recalling that Hr = H(ai/ar)1/α, we also have that Eq. (8.10) implies

Using Eq. (8.11) and the definition of Σ (see Eq. (8.3)) it turns out that Σ = λ1/4, which is always smaller than 1 and, at most,  (1).
(1).
Instead of endorsing an explicit model by pretending to know the whole thermal history of the Universe in reasonable detail, it is more productive to keep Σ as a free parameter and to require that the scaling violations in the spectral energy density will take place before BBN. Consequently the variation of Σ, w and rT can be simultaneously bounded [46, 47]. If the stiff dynamics takes place before big-bang nucleosynthesis, then νs > νbbn (see also Eq. (6.61)). This requirement guarantees that the stiff dynamics will be over by the time light nuclei start being formed. In a complementary approach one might also require that νs > νew where νew corresponds to the value of the Hubble rate at the electroweak epoch, i.e.


Finally, yet a different requirement could be to impose that ν > νTev where νTeV is defined as

The latter requirement would imply that the stiff age is already finished by the time the Universe has a temperature of the order of 100 TeV when, presumably, the number of relativistic degrees of freedom was much larger than in the minimal standard model (in Eq. (8.14) the typical value of g ρ is the one arising in the minimal supersymmetric extension of the standard model).
In Fig. 14 (plot at the left) the constraints on Σ, wt are illustrated. The value of Σ controls the position of the frequency at which the nearly scale-invariant slope of the spectrum will be violated. The barotropic index wt is taken to be always larger than 1/3 and with a maximal value of 1. The shaded region corresponds to the region excluded in the most constraining case, i.e. the one demanding νs > νbbn. Also the values of rT are bounded by the same kind of considerations. Indeed, νs depends upon ϵ which is related to rT (see, e.g., Eq. (8.7)). Therefore, a lower bound on νs also implies a bound in the (rT, wt) plane.
8.2 Spectral energy density in the minimal TΛCDM scenario
In Fig. 14 (plot at the right) two examples of the scaling violations on the spectral energy density are illustrated. Both examples are compatible with the bounds illustrated in the plot at the left. Similar examples have been already illustrated in Fig. 4. These examples will now be discussed in greater detail. The spectral energy density has been computed by using the numerical approach presented in section 6.
In the two examples of Fig. 14 (plot at the right) the ΛCDM parameters are fixed to the values reported in Eq. (2.7) (see [3–7]). The spectral index has been allowed to run, i.e. αT ≠ 0 (see Eqs. (1.6) and (6.53)). The two supplementary parameters should be identified with the sound speed during the stiff phase (i.e. cst) and the threshold frequency (i.e. νs). Besides cst and νs, there will also be rT which controls, at once, the normalization and the slope of the low-frequency branch of the spectral energy density. At the moment wide band interferometers have sensitivities which are insufficient for cutting through the phenomenologically interesting region [69–71]. In the near future, however, there is the hope of a dramatic improvement of the sensitivity: even 5 or 6 orders of magnitude at least heeding the original design (see e.g. [61]) together with the recent proposals for an advanced Ligo program.
As specifically discussed in Eqs. (8.5)-(8.6) the frequency of the elbow, i.e. νs, is fully determined by Σ (see Eq. (8.3) and discussion therein). The two supplementary parameters νs and cst can be traded for Σ and wt as already done in Fig. 14 (plot at the left). In doing so there is also a potential advantage since, according to Eq. (8.4), Σ shifts the maximal frequency of the spectrum.
As soon as the frequency increases from the aHz up to the nHz (and even larger) the spectral energy density increases sharply in comparison with the nearly scale-invariant case where the spectral energy density was, for ν > nHz, at most  (10-16). In the case of Fig. 14 the spectral energy density is clearly much larger. The accuracy in the determination of the infra-red branch of the spectrum is a condition for the correctness of the estimate of the spectral energy density of the high-frequency branch. The plots of Fig. 14 (see also Fig. 4) demonstrate that the low-frequency bounds on rT do not forbid a larger signal at higher frequencies.
(10-16). In the case of Fig. 14 the spectral energy density is clearly much larger. The accuracy in the determination of the infra-red branch of the spectrum is a condition for the correctness of the estimate of the spectral energy density of the high-frequency branch. The plots of Fig. 14 (see also Fig. 4) demonstrate that the low-frequency bounds on rT do not forbid a larger signal at higher frequencies.
A decrease of rT implies a suppression of the nearly scale-invariant plateau in the region νeq <ν <νs. At the same time the amplitude of the spectral energy density still increases for frequencies larger than the frequency of the elbow (i.e. νs). The latter trend can be simply understood since, at high frequency, the transfer function for the spectral energy density grows faster than the power spectrum of inflationary origin. For instance, in the case wt = 1 and neglecting logarithmic corrections,  for ν ≫ νs. Now, recall that nT is given by Eq. (1.4). If rT → 0, the combination (nT + 1) will be much closer to 1 than in the case when, say, rT ≃ 0.3. This aspect can be observed in Fig. 4 where different values of rT have been reported. By decreasing the wt from 1 to, say, 0.6 the extension of the nearly flat plateau gets narrower. This is also a general effect which is particularly evident by comparing the two curves of Fig. 14 (plot at the right).
for ν ≫ νs. Now, recall that nT is given by Eq. (1.4). If rT → 0, the combination (nT + 1) will be much closer to 1 than in the case when, say, rT ≃ 0.3. This aspect can be observed in Fig. 4 where different values of rT have been reported. By decreasing the wt from 1 to, say, 0.6 the extension of the nearly flat plateau gets narrower. This is also a general effect which is particularly evident by comparing the two curves of Fig. 14 (plot at the right).
The slope of the high-frequency branch of the graviton energy spectrum can be easily deduced with analytic methods and it turns out to to be

up to logarithmic corrections. The result of Eq. (8.15) stems from the simultaneous integration of the background evolution equations and of the tensor mode functions according to the techniques described in section 3. The semi-analytic estimate of the slope (see [82]) agrees with the results obtained by means of the transfer function of the spectral energy density.
To conclude the discussion it is appropriate to elaborate on the interplay between the stiff spectra and the phenomenological bounds mentioned in subsection 1.6. Let us start with millisecond pulsar bound of Eq. (1.14).
Assuming the maximal growth of the spectral energy density and the minimal value of νs, i.e. νbbn we will have

Since νpulsar ≃ 103 νbbn, Eq. (8.16) implies that  (νpulsar, τ0) ≃ 10-13or even 10-14 depending upon rT. But this value is always much smaller than the constraint stemming from pulsar timing measurements (see Eq. (1.14)). If either νs ≫ νbbn or cst < 1 the value of
(νpulsar, τ0) ≃ 10-13or even 10-14 depending upon rT. But this value is always much smaller than the constraint stemming from pulsar timing measurements (see Eq. (1.14)). If either νs ≫ νbbn or cst < 1 the value of  (νpulsar, τ0) will be even smaller. This conclusion follows immediately from the hierarchy between νpulsar and νbbn. If either νs ≫ νbbn,
(νpulsar, τ0) will be even smaller. This conclusion follows immediately from the hierarchy between νpulsar and νbbn. If either νs ≫ νbbn,  can only grow very little and certainly much less than required to violate the bound of Eq. (1.14). Consequently, even in the extreme cases when the frequency of the elbow is close to νbbn, the spectral energy density is always much smaller than the requirement of Eq. (1.14).
can only grow very little and certainly much less than required to violate the bound of Eq. (1.14). Consequently, even in the extreme cases when the frequency of the elbow is close to νbbn, the spectral energy density is always much smaller than the requirement of Eq. (1.14).
As noticed in the past [82], the most significant constraint on the stiff spectra stems from BBN. The models illustrated in Fig. 14 (plot at the right) are on the verge of saturating the bounds of Eqs. (1.18)-(1.19). This conclusion stems directly from the form of spectral energy density: the broad spike dominates the (total) energy density of relic gravitons which are inside the Hubble radius at the time of big bang nucleosynthesis. For consistency with the low-frequency determinations of the tensor power spectrum rT must be bounded from above according to the values reported, for instance, in Tabs. 1 and 2. Once the the value of rT has been selected, the constraints of Eqs. (1.18)-(1.19) can be imposed. From Fig. 14 a large signal is expected for νLV ≃ 100 Hz for 0.35 <wt < 0.6. This range turns out to be compatible with the bounds of Eqs. (1.18)-(1.19). In the opposite limit (e. g. wt ≃ 1) the spike becomes narrower, the elbow frequency augments and the signal at the interferometer scale diminishes.
In Fig. 15 the energy density of the relic gravitons inside the Hubble radius at the nucleosynthesis epoch is reported in the case rT = 0.1 and for different values of Σ. In the plot at the left ns = 0.963 as implied by the WMAP 5-yr data alone. The acceptable region of the parameter space must stay below the horizontal lines which illustrate different values of ΔN ν (see Eqs. (1.18)-(1.19)). As the scalar spectral index diminishes, the constraints are better satisfied since ns controls αT and, consequently, the frequency dependence of the tensor spectral index nT (see Eq. (1.4)) in the case αT ≠ 0.
The bounds stemming from the amount of extra-relativistic species at the epoch of the synthesis of light nuclei are applied to the relic graviton spectra from the stiff epoch (plot at the left). The detectability constraint (full line in the plot at the right) stemming from the putative sensitivities of wide-band interferometers in their advanced version. The points corresponding to the spectral energy density should lie above the full lines to be potentially interesting for those instruments.
8.3 Detectability prospects
By lowering wt,  (ν, τ0) increases for ν = νLV ≃ 0.1 kHz. This trend can be inferred from Fig. 15 (plot at the right) where the spectral energy density is evaluated exactly for ν = νLV. To be detectable by wide band interferometers the parameters of the TΛCDM must lie above the full lines. The region of low barotropic indices emerging neatly from Fig. 15, leads to spectral energy densities which are progressively flattening as wt diminishes towards 1/3. Low values of wt bring the frequency of the elbow, i.e. νs below 10-10 Hz which is unacceptable since it would mean that, during nucleosynthesis, the Universe was dominated by the stiff fluid. In Fig. 14 (plot at the left) the region above the full line corresponds to a range of parameters for which νs > νbbn: in such a range a decrease of wt demands an increase of Σ. The latter occurrence is illustrated in Fig. 16 where, at the left, wt = 0.5. The full, dashed and dot-dashed curves illustrated in Fig. 16 (plot at the left) are incompatible with the phenomenological constraints since the frequency of the elbow is systematically smaller than νbbn. Once more, this choice of parameters would contradict the bounds of Fig. 14 and would imply that the stiff phase is not yet finished at the BBN time. In the left plot of Fig. 16 the diamonds denote a model which is compatible with BBN considerations but whose signal at the frequency of interferometers is rather small (always three orders of magnitude larger than in the case of conventional inflationary models).
(ν, τ0) increases for ν = νLV ≃ 0.1 kHz. This trend can be inferred from Fig. 15 (plot at the right) where the spectral energy density is evaluated exactly for ν = νLV. To be detectable by wide band interferometers the parameters of the TΛCDM must lie above the full lines. The region of low barotropic indices emerging neatly from Fig. 15, leads to spectral energy densities which are progressively flattening as wt diminishes towards 1/3. Low values of wt bring the frequency of the elbow, i.e. νs below 10-10 Hz which is unacceptable since it would mean that, during nucleosynthesis, the Universe was dominated by the stiff fluid. In Fig. 14 (plot at the left) the region above the full line corresponds to a range of parameters for which νs > νbbn: in such a range a decrease of wt demands an increase of Σ. The latter occurrence is illustrated in Fig. 16 where, at the left, wt = 0.5. The full, dashed and dot-dashed curves illustrated in Fig. 16 (plot at the left) are incompatible with the phenomenological constraints since the frequency of the elbow is systematically smaller than νbbn. Once more, this choice of parameters would contradict the bounds of Fig. 14 and would imply that the stiff phase is not yet finished at the BBN time. In the left plot of Fig. 16 the diamonds denote a model which is compatible with BBN considerations but whose signal at the frequency of interferometers is rather small (always three orders of magnitude larger than in the case of conventional inflationary models).
The compatibility with the phenomenological constraints demands that the parameters of the TΛCDM paradigm must lie above the full lines of Fig. 14 (plot at the left). The requirements of Fig. 14 suggest, therefore, that Σ should be raised a bit. In this case the frequency of the elbow gets shifted to the right but, at the same time, the overall amplitude of the spike diminishes. The putative amplitude remains still much larger than the conventional inflationary signal reported, for instance, in Fig. 3.
In Fig. 17 the spectral energy density of the relic gravitons is illustrated as a function of rT for a choice of parameters which is compatible with all the bounds applicable to the stochastic backgrounds of the relic gravitons. The three curves refer to three different frequencies, i.e. 0.1 kHz, 1 kHz and 10 kHz. Indeed, if the spectrum is nearly scale-invariant (as in the case o Fig. 3) we can compare the potential signal with the central frequency of the window. If the signal increases with frequency it is interesting to plot the same curve for some significant frequencies inside the window of wide-band interferometers. Even if the frequency window extends from few Hz to 10 kHz the maximal sensitivity is in the central region and depends upon various important factors which will now be briefly discussed.
To illustrate more quantitatively this point we remind the expression of the signal-to-noise ratio (SNR) in the context of optimal processing required for the detection of stochastic backgrounds:

(F depends upon the geometry of the two detectors and in the case of the correlation between two interferometers F = 2/5; T is the observation time). In Eq. (8.17),  (f) is the (one-sided) noise power spectrum (NPS) of the k-th (k = 1, 2) detector. The NPS contains the important informations concerning the noise sources (in broad terms seismic, thermal and shot noises) while γ (ν) is the overlap reduction function which is determined by the relative locations and orientations of the two detectors. In [74] Eq. (8.17) has been used to assess the detectability prospects of gravitons coming from a specific model of stiff evolution with wt = 1. At that time the various suppressions of the low-frequency amplitude as well as the free-streaming effects were not taken into account. Furthermore, the evaluation of the energy transfer function was obtained, in [76], not numerically but by matching of the relevant solutions. We do know, by direct comparison, that such a procedure is justified but intrinsically less accurate than the one proposed here. It would be interesting to apply Eq. (8.17) for the (more accurate) assessment of the sensitivities of different instruments to a potential signal stemming from the stiff age.
(f) is the (one-sided) noise power spectrum (NPS) of the k-th (k = 1, 2) detector. The NPS contains the important informations concerning the noise sources (in broad terms seismic, thermal and shot noises) while γ (ν) is the overlap reduction function which is determined by the relative locations and orientations of the two detectors. In [74] Eq. (8.17) has been used to assess the detectability prospects of gravitons coming from a specific model of stiff evolution with wt = 1. At that time the various suppressions of the low-frequency amplitude as well as the free-streaming effects were not taken into account. Furthermore, the evaluation of the energy transfer function was obtained, in [76], not numerically but by matching of the relevant solutions. We do know, by direct comparison, that such a procedure is justified but intrinsically less accurate than the one proposed here. It would be interesting to apply Eq. (8.17) for the (more accurate) assessment of the sensitivities of different instruments to a potential signal stemming from the stiff age.
For intermediate frequencies the integral of Eq. (8.17) is sensitive to the form of the overlap reduction function which depends upon the mutual position and relative orientations of the interferometers. The function γ (ν) effectively cuts-off the integral which defines the signal to noise ratio for a typical frequency ν ≃1/(2d) where d is the separation between the two detectors. Since ΩGW increases with frequency (at least in the case of relic gravitons from stiff ages) at most as ν and since there is a ν-6 in the denominator, the main contribution to the integral should occur for ν < 0.1 kHz. This argument can be explicit verified in the case of the calculations carried on in [74] and it would be interesting to check it also in our improved framework.
Equation (8.17) assumes that the intrinsic noises of the detectors are stationary, Gaussian, uncorrelated, much larger in amplitude than the gravitational strain, and statistically independent on the strain itself [77, 78, 80, 81]. The integral appearing in Eq. (8.17) extends over all the frequencies. However, the noise power spectra of the detectors are defined in a frequency interval ranging from few Hz to 10 kHz. In the latter window, for very small frequencies the seismic disturbances are the dominant source of noise. For intermediate and high frequencies the dominant sources of noise are, respectively, thermal and electronic (i.e. shot) noises. The wideness of the band is very important when cross-correlating two detectors: typically the minimal detectable  will become smaller (i.e. the sensitivity will increase) by a factor 1/
will become smaller (i.e. the sensitivity will increase) by a factor 1/ where Δν is the bandwidth and T, as already mentioned, is the observation time. Naively, if the minimal detectable signal (by one detector) is
where Δν is the bandwidth and T, as already mentioned, is the observation time. Naively, if the minimal detectable signal (by one detector) is  ≃ 10-5, then the cross-correlation of two identical detector with overlap reduction γ (ν) = 1 will detect
≃ 10-5, then the cross-correlation of two identical detector with overlap reduction γ (ν) = 1 will detect  ≃ 10-10 provided Δν ≃ 100 Hz and T ≃
≃ 10-10 provided Δν ≃ 100 Hz and T ≃  (1 yr) (recall that 1 yr = 3.15 × 107Hz-1). The achievable sensitivity of a pair of wide band interferometers crucially depends upon the spectral slope of the theoretical energy spectrum in the operating window of the detectors. So, a at spectrum will lead to an experimental sensitivity which might not be similar to the sensitivity achievable in the case of a blue or violet spectra. Previous calculations [74–76] showed that, however, to get a reasonable idea of the potential signal it is sufficient to compare the signal with the sensitivity to at spectrum which has been reported in Eq. (1.13). Of course any experimental improvement in comparison with the values of Eq. (1.13) will widen the detectability region by making the prospects of the whole discussion more rosy.
(1 yr) (recall that 1 yr = 3.15 × 107Hz-1). The achievable sensitivity of a pair of wide band interferometers crucially depends upon the spectral slope of the theoretical energy spectrum in the operating window of the detectors. So, a at spectrum will lead to an experimental sensitivity which might not be similar to the sensitivity achievable in the case of a blue or violet spectra. Previous calculations [74–76] showed that, however, to get a reasonable idea of the potential signal it is sufficient to compare the signal with the sensitivity to at spectrum which has been reported in Eq. (1.13). Of course any experimental improvement in comparison with the values of Eq. (1.13) will widen the detectability region by making the prospects of the whole discussion more rosy.
In the TΛCDM paradigm the maximal signal occurs in a frequency region between the MHz and the GHz. This intriguing aspect led to the suggestion [74, 75] that microwave cavities [158] can be used as GW detectors precisely in the mentioned frequency range. Prototypes of these detectors [159, 160] have been described and the possibility of further improvements in their sensitivity received recently attention [161–166]. Different groups are now concerned with high-frequency gravi-tons. In [162] the ideas put forward in [158, 159, 161] have been developed by using electromagnetic cavities (i.e. static electromagnetic fields). In [163–165] dynamical electromagnetic fields (i.e. wave guides) have been studied always for the purpose of detecting relic gravitons. Yet a different approach to the problem has been described in [166]. In [165] an interesting prototype detector was described with frequency of operation of the order of 100 MHz (see also [167]). It is not clear if, in the near future, the improvements in the terrestrial technologies will allow the detection of relic gravitons for frequencies, say, larger than the MHz. It is, however, a rather intriguing possibility.
9 Final remarks
The incoming score year might witness direct experimental evidences of relic gravitons either from small frequency experiments or from high-frequency experiments. By low-frequency experiments we mean, as in the bulk of this review, the CMB experiments possibly analyzed together with the two remaining cosmological data sets (i.e. large-scale structure determinations of the matter power spectrum and type Ia supernova observations). By high-frequency experiments we mean the appropriately advanced versions of wide band interferometers such as Ligo, Virgo, Geo and Tama.
The main observables related to relic gravitons have been reviewed in a self-contained manner and in the framework of the ΛCDM paradigm with specific attention to the complementarity between the low-frequency and the high-frequency branches of the relic graviton spectrum. Any model claiming a signal coming from high-frequency gravitons should be compatible with the ΛCDM paradigm in the low-frequency branch of the relic graviton spectrum.
It is instructive to go back to the comparison drawn, in Fig. 1, between the electromagnetic spectrum and the relic graviton spectrum. The gap between the graviton frequencies explored by CMB experiments and the graviton frequencies probed by wide-band interferometers is of the order of the frequency gap between radio waves and γ-rays.
A detection of long wavelength gravitons in CMB experiments can be direct (i.e. from the B-mode polarization) or indirect (i.e. from some global fit of CMB observables including the tensor contribution). In the context of the ΛCDM paradigm the CMB detection of long wavelength gravitons will fix the overall normalization of the spectral energy density. Even in the absence of such a direct detection, the current upper limits on the contribution of long wavelength gravitons to CMB observables implies a minute signal at higher frequencies. The (hoped) sensitivities achievable by the advanced wide-band interferometers are still insufficient for a direct detection of high-frequency gravitons.
The latter statement summarizes the standard lore of the problem which may well be realized. At the same time it might be unwise to assume (or presume) that the current success of the ΛCDM paradigm also fixes the whole thermal history of the Universe for temperatures larger than the MeV. The general ideas conveyed in the present review suggest that the high-frequency branch of the relic graviton spectrum is rather sensitive to the whole post-inflationary thermal history of the Universe. If the post-inflationary evolution is dominated by stiff sources, for instance, it is not impossible, as explicitly shown, to have positive detection of relic gravitons both at small and high frequencies even enforcing the current bounds on the tensor contribution to CMB observables.
If we assume (or strongly believe) the standard lore (i.e. that relic gravitons will probably not be seen by wide-band detectors) it is useless to demand theoretical accuracy. For instance it is useless to ask what would be the effect of changing ΩΛ on a signal which is anyway 6 or even 7 orders of magnitude smaller than the most optimistic sensitivities. A positive detection of relic graviton backgrounds at high-frequencies would demand, however, more accurate estimates of the theoretical signal in different models. Absent a direct detection of relic gravitons by wide-band inteferometers, accurate theoretical calculations can be used to set bounds on possible deviations of the post-inflationary thermal history.
References
Smoot GF: Rev Mod Phys. 2007, 79: 1349-10.1103/RevModPhys.79.1349.
Songaila A, et al: Nature. 1994, 371: 43-10.1038/371043a0.
Hinshaw G, [WMAP Collaboration], et al: Astrophys J Suppl. 2009, 180: 225-10.1088/0067-0049/180/2/225.
Dunkley J, [WMAP Collaboration], et al: Astrophys J Suppl. 2009, 180: 306-10.1088/0067-0049/180/2/306.
Gold B, [WMAP Collaboration], et al: Astrophys J Suppl. 2009, 180: 265-10.1088/0067-0049/180/2/265.
Komatsu E, [WMAP Collaboration], et al: Astrophys J Suppl. 2009, 180: 330-10.1088/0067-0049/180/2/330.
Nolta MR, [WMAP Collaboration], et al: Astrophys J Suppl. 2009, 180: 296-10.1088/0067-0049/180/2/296.
Spergel DN, [WMAP Collaboration], et al: Astrophys J Suppl. 2003, 148: 175-10.1086/377226.
Peiris HV, [WMAP Collaboration], et al: Astrophys J Suppl. 2003, 148: 213-10.1086/377228.
Bennett CL, [WMAP Collaboration], et al: Astrophys J Suppl. 2003, 148: 1-10.1086/377253.
Spergel DN, [WMAP Collaboration], et al: Astrophys J Suppl. 2007, 170: 377-10.1086/513700.
Page L, [WMAP Collaboration], et al: Astrophys J Suppl. 2007, 170: 335-10.1086/513699.
Freedman WL, et al: Astrophys J. 2001, 553: 47-10.1086/320638.
Cole S, [The 2dFGRS Collaboration], et al: Mon Not Roy Astron Soc. 2005, 362: 505-10.1111/j.1365-2966.2005.09318.x.
Eisenstein DJ, [SDSS Collaboration], et al: Astrophys J. 2005, 633: 560-10.1086/466512.
Tegmark M, [SDSS Collaboration], et al: Astrophys J. 2004, 606: 702-10.1086/382125.
Astier P, [The SNLS Collaboration], et al: Astron Astrophys. 2006, 447: 31-10.1051/0004-6361:20054185.
Riess AG, [Supernova Search Team Collaboration], et al: Astrophys J. 2004, 607: 665-10.1086/383612.
Barris BJ, et al: Astrophys J. 2004, 602: 571-10.1086/381122.
Montroy TE, et al: Astrophys J. 2006, 647: 813-10.1086/505560.
Kuo Cl, et al: Astrophys J. 2004, 600: 32-10.1086/379783.
Readhead ACS, et al: Astrophys J. 2004, 609: 498-10.1086/421105.
Dickinson C: Mon Not Roy Astron Soc. 2004, 353: 732-10.1111/j.1365-2966.2004.08206.x.
Kovac JM, et al: Nature. 2002, 420: 772-10.1038/nature01269.
Leitch EM, et al: Astrophys J. 2005, 624: 10-10.1086/428825.
Bernardi G, et al: Mon Not R Astron Soc. 2006, 370: 2064-
Barkats D, et al: Astrophys J. 2005, 619: L127-10.1086/428285.
Bischoff C, et al: Astrophys J. 2008, 684: 771-10.1086/590487.
Readhead ACS, et al: arXiv:astro-ph/0409569.
Sievers JL, et al: Astrophys J. 2008, 660: 976-10.1086/510504.
Ade P, [QUaD collaboration], et al: Astrophys J. 2008, 674: 22-10.1086/524922.
Pryke C, [QUaD collaboration], et al: arXiv:0805.1944 [astro-ph].
Wu EYS, [QUaD collaboration], et al: arXiv:0811.0618 [astro-ph].
Chiang HC, et al: arXiv:0906.1181 [astro-ph.CO].
Takahashi YD, et al: arXiv:0906.4069 [astro-ph.CO].
Taylor A, et al: New Astron Rev. 2006, 50: 993-10.1016/j.newar.2006.09.026.
Polenta G, et al: New Astron Rev. 2007, 51: 256-10.1016/j.newar.2006.11.065.
QUIET experiment. [http://quiet.uchicago.edu/]
Crill BP, et al: arXiv:0807.1548 [astro-ph].
Oxley P, et al: Proc SPIE Int Soc Opt Eng. 2004, 5543: 320-[arXiv:astro-ph/0501111].
Planck explorer satellite. [http://www.rssd.esa.int/index.php?project=PLANCK]
Weinberg S: Phys Rev D. 2004, 69: 023503-10.1103/PhysRevD.69.023503.
Dicus DA, Repko WW: Phys Rev D. 2005, 72: 088302-10.1103/PhysRevD.72.088302.
Boyle LA, Steinhardt PJ: Phys Rev D. 2008, 77: 063504-10.1103/PhysRevD.77.063504.
Watanabe Y, Komatsu E: Phys Rev D. 2006, 73: 123515-10.1103/PhysRevD.73.123515.
Giovannini M: Phys Lett B. 2008, 668: 44-10.1016/j.physletb.2008.07.107.
Giovannini M: Class Quant Grav. 2009, 26: 045004-10.1088/0264-9381/26/4/045004.
Grishchuk LP: Zh Éksp Teor Fiz. 1974, 67: 825-[Sov. Phys. JETP 40, 409. (1975)].
Starobinsky AA: JETP Lett. 1979, 30: 682-
Rubakov VA, Sazhin MV, Veryaskin AV: Phys Lett. 1982, 115B: 189-
Fabbri R, Pollock MD: Phys Lett. 1983, 125B: 445-
Abbott LF, Wise MB: Nucl Phys. 1984, 224: 541-10.1016/0550-3213(84)90329-8.
Allen B: Phys Rev D. 1988, 37: 2078-10.1103/PhysRevD.37.2078.
Sahni V: Phys Rev D. 1990, 42: 453-10.1103/PhysRevD.42.453.
Grishchuk LP, Solokhin M: Phys Rev D. 1991, 43: 2566-10.1103/PhysRevD.43.2566.
Gasperini M, Giovannini M: Phys Lett. 1992, 282B: 36-
Thorne KS: 300 Years of Gravitation. Edited by: Hawking SW, Israel W. 1987, Cambridge University Press, Cambridge, England
Grishchuk LP: Usp Fiz Nauk. 1988, 156: 297-[Sov. Phys. Usp. 31, 940. (1988)].
Allen B: Proc of the Les Houches School on Astrophysical Sources of Gravitational Waves. Edited by: Marck J, Lasota JP. 1996, Cambridge University Press, Cambridge England
Grishchuk LP: Class Quant Grav. 1993, 10: 2449-10.1088/0264-9381/10/12/006.
Abramovici A, et al: Science. 1992, 256: 325-10.1126/science.256.5055.325.
Caron B, et al: Class Quant Grav. 1997, 14: 1461-
Ando M, et al: Phys Rev Lett. 2001, 86: 3950-10.1103/PhysRevLett.86.3950.
Lück H, et al: Class Quant Grav. 1997, 14: 1471-10.1088/0264-9381/14/6/012.
Saulson PR: Fundamentals of interferometric gravitational wave detectors. 1994, World Scientific, Singapore
Laser Interferometric Space Antenna. [http://www.lisa-science.org]
Harry GM, Fritschel P, Shaddock DA, Folkner W, Phinney ES: Class Quant Grav. 2006, 23: 4887-10.1088/0264-9381/23/15/008. [Erratum-ibid. 23, 7361 (2006)].
Kawamura S, et al: Class Quant Grav. 2006, 23: S125-10.1088/0264-9381/23/8/S17.
Abbott B, [LIGO Collaboration], et al: Astrophys J. 2007, 659: 918-10.1086/511329.
Abbott B, [LIGO Scientific Collaboration], et al: Phys Rev D. 2007, 76: 082003-10.1103/PhysRevD.76.082003.
Abbott B, [ALLEGRO Collaboration and LIGO Scientific Collaboration], et al: Phys Rev D. 2007, 76: 022001-10.1103/PhysRevD.76.022001.
Cella G, Colacino CN, Cuoco E, Di Virgilio A, Regimbau T, Robinson EL, Whelan JT: Class Quant Grav. 2007, 24: S639-10.1088/0264-9381/24/19/S26.
Baggio L, [AURIGA Collaboration], et al: Class Quant Grav. 2008, 25: 095004-10.1088/0264-9381/25/9/095004.
Babusci D, Giovannini M: Phys Rev D. 1999, 60: 083511-10.1103/PhysRevD.60.083511.
Babusci D, Giovannini M: Class QuantGrav. 2000, 17: 2621-10.1088/0264-9381/17/14/302.
Babusci D, Giovannini M: Int J Mod PhysD. 2001, 10: 477-
Michelson P: Mon Not R Astron Soc. 1987, 227: 933-
Christensen N: Phys Rev D. 1992, 46: 5250-10.1103/PhysRevD.46.5250.
Christensen N: Phys Rev D. 1997, 55: 448-10.1103/PhysRevD.55.448.
Flanagan E: Phys Rev D. 1993, 48: 2389-10.1103/PhysRevD.48.2389.
Allen B, Romano J: Phys Rev D. 1999, 59: 102001-10.1103/PhysRevD.59.102001.
Giovannini M: Phys Rev D. 1998, 58: 083504-10.1103/PhysRevD.58.083504.
Giovannini M: Class Quant Grav. 1999, 16: 2905-10.1088/0264-9381/16/9/308.
Giovannini M: Phys Rev D. 1999, 60: 123511-10.1103/PhysRevD.60.123511.
Peebles PJE, Vilenkin A: Phys Rev D. 1999, 59: 063505-10.1103/PhysRevD.59.063505.
Kaspi VM, Taylor JH, Ryba MF: Astrophys J. 1994, 428: 713-10.1086/174280.
Jenet FA, et al: Astrophys J. 2006, 653: 1571-10.1086/508702. [arXiv:astro-ph/0609013].
Schwartzmann VF: JETP Lett. 1969, 9: 184-
Giovannini M, Kurki-Suonio H, Sihvola E: Phys Rev D. 2002, 66: 043504-10.1103/PhysRevD.66.043504.
Cyburt RH, Fields BD, Olive KA, Skillman E: Astropart Phys. 2005, 23: 313-10.1016/j.astropartphys.2005.01.005.
Jackson JD: Classical Electrodynamics. 1975, Wiley, New York
Blatt JM, Weisskopf VF: Theoretical Nuclear Physics. 1952, John Wiley and Sons, New York, 798-
Edmonds AR: Angular Momentum in Quantum Mechanics. 1968, Princeton University Press, Princeton, New Jersey, 81-
Biedenharn LC, Louck JD: Angular Momentum in Quantum Physics. 1981, Addison-Wesley, Reading, Massachusetts, 442-
Varshalovich DA, Moskalev AN, Khersonskii VK: Quantum Theory of Angular Momentum. 1988, World Scientific, Singapore, 228-
Newman E, Penrose R: J Math Phys. 1966, 7: 863-10.1063/1.1931221.
Goldberg J, Macfarlane A, Newman E, Rohrlich F, Sudarshan E: J Math Phys. 1966, 7: 863-10.1063/1.1704951.
Zaldarriaga M, Seljak U: Phys Rev D. 1997, 55: 1830-10.1103/PhysRevD.55.1830.
Hu W, White MJ: Phys Rev D. 1997, 56: 596-10.1103/PhysRevD.56.596.
Kamionkowski M, Kosowsky A, Stebbins A: Phys Rev D. 1997, 55: 7368-10.1103/PhysRevD.55.7368.
Cabella P, Kamionkowski M: arXiv:astro-ph/0403392.
Pritchard JR, Kamionkowski M: Annals Phys. 2005, 318: 2-10.1016/j.aop.2005.03.005.
Sakurai JJ: Modern Quantum Mechanics. 1985, Addison-Wesley, New York
Loudon R: The Quantum Theory of Light. 1991, Oxford University Press
Mandel L, Wolf E: Optical Coherence and Quantum optics. 1995, Cambridge University Press, Cambridge, England
Gasperini M, Giovannini M: Phys Lett B. 1993, 301: 334-10.1016/0370-2693(93)91159-K.
Gasperini M, Giovannini M, Veneziano G: Phys Rev D. 1993, 48: 439-10.1103/PhysRevD.48.R439.
Gasperini M, Giovannini M: Class Quant Grav. 1993, 10: L133-10.1088/0264-9381/10/9/004.
Polarski D, Starobinsky AA: Class Quant Grav. 1996, 13: 377-10.1088/0264-9381/13/3/006.
Kiefer C, Polarski D, Starobinsky AA: Int J Mod Phys D. 1998, 7: 455-10.1142/S0218271898000292.
Barut AO, Girardello L: Commun Math Phys. 1971, 21: 41-10.1007/BF01646483.
Stoler D: Phys Rev D. 1970, 1: 3217-10.1103/PhysRevD.1.3217.
Yuen HP: Phys Rev A. 1976, 13: 2226-10.1103/PhysRevA.13.2226.
Shumaker BL: Phys Rep. 1986, 135: 317-10.1016/0370-1573(86)90179-1.
Grochmalicki J, Lewenstein M: Phys Rep. 1991, 208: 189-10.1016/0370-1573(91)90100-Z.
Ford LH, Parker L: Phys Rev D. 1977, 16: 1601-10.1103/PhysRevD.16.1601.
Ford LH, Parker L: Phys Rev D. 1977, 16: 245-10.1103/PhysRevD.16.245.
Lifshitz EM, Landau LD: The Classical Theory of Fields. 1975, Pergamon Press, Oxford
Isaacson R: Phys Rev. 1968, 166: 1263-10.1103/PhysRev.166.1263.
Isaacson R: Phys Rev. 1968, 166: 1272-10.1103/PhysRev.166.1272.
Mukhanov VF, Abramo LRW, Brandenberger RH: Phys Rev Lett. 1997, 78: 1624-10.1103/PhysRevLett.78.1624. Phys. Rev. D 56, 1997, 3248.
Abramo LR: Phys Rev D. 1999, 60: 064004-10.1103/PhysRevD.60.064004.
Babak SV, Grishchuk LP: Phys Rev D. 2000, 61: 024038-10.1103/PhysRevD.61.024038.
Giovannini M: Phys Rev D. 2006, 73: 083505-10.1103/PhysRevD.73.083505.
Abramowitz M, Stegun IA: Handbook of Mathematical Functions. 1972, Dover, New York
Erdelyi A, Magnus W, Obehettinger F, Tricomi F: Higher Trascendental Functions. 1953, McGraw-Hill, New York
Giovannini M: A Primer on the Physics of the Cosmic Microwave Background. 2008, World Scientific, Singapore
Turner MS, White MJ, Lidsey JE: Phys Rev D. 1993, 48: 4613-10.1103/PhysRevD.48.4613.
Zeldovich YB: Mon Not Roy Astron Soc. 1972, 160: 1P-
Grishchuk LP: Ann (NY) Acad Sci. 1977, 302: 439-10.1111/j.1749-6632.1977.tb37064.x.
Spokoiny B: Phys Lett B. 1993, 315: 40-10.1016/0370-2693(93)90155-B.
Ellis G, Maartens R, MacCallum MAH: Gen Rel Grav. 2007, 39: 1651-10.1007/s10714-007-0479-2.
Babichev E, Mukhanov V, Vikman A: JHEP. 2008, 0802: 101-10.1088/1126-6708/2008/02/101.
Giovannini M: Phys Rev D. 2008, 78: 087301-10.1103/PhysRevD.78.087301.
Ford LH: Phys Rev D. 1987, 35: 2955-10.1103/PhysRevD.35.2955.
Birrel ND, Davies PCW: Quantum fields in curved space. 1982, Cambridge University Press, Cambridge
Garriga J, Verdaguer E: Phys Rev D. 1991, 39: 1072-10.1103/PhysRevD.39.1072.
Chongchitnan S, Efstathiou G: Phys Rev D. 2006, 73: 083511-10.1103/PhysRevD.73.083511.
Page L, [WMAP Collaboration], et al: Astrophys J Suppl. 2007, 170: 335-10.1086/513699.
Zhao W, Zhang Y: Phys Rev D. 2006, 74: 043503-10.1103/PhysRevD.74.043503.
Zhang Y, Yuan Y, Zhao W, Chen YT: Class Quant Grav. 2005, 22: 1383-10.1088/0264-9381/22/7/011.
Zhang Y, Er XZ, Xia TY, Zhao W, Miao HX: Class Quant Grav. 2006, 23: 3783-10.1088/0264-9381/23/11/007.
Polnarev A: Sov Astron. 1985, 29: 6-
Harari D, Zaldarriaga M: Phys Lett B. 1993, 310: 96-
Ng KL, Ng KW: Astrophys J. 1995, 445: 521-10.1086/175717.
Keating B, et al: Astrophys J. 1998, 495: 580-10.1086/305312.
Sunyaev RA, Zeldovich YB: Astrophys Space Sci. 1970, 7: 3-
Jones B, Wyse R: Astron Astrophys. 1985, 149: 144-
Naselsky P, Novikov I: Astrophys J. 1993, 413: 14-10.1086/172972.
Jorgensen H, Kotok E, Naselsky P, Novikov I: Astron Astrophys. 1995, 294: 639-
Sahni V, Sami M, Souradeep T: Phys Rev D. 2002, 65: 023518-10.1103/PhysRevD.65.023518.
Tashiro H, Chiba T, Sasaki M: Class Quant Grav. 2004, 21: 1761-10.1088/0264-9381/21/7/004.
Battefeld TJ, Easson DA: Phys Rev D. 2004, 70: 103516-10.1103/PhysRevD.70.103516.
Giovannini M: Phys Rev D. 1999, 59: 121301-10.1103/PhysRevD.59.121301.
Giovannini M: Phys Rev D. 2000, 61: 108302-10.1103/PhysRevD.61.108302.
Cataldo M, Mella P: Phys Lett B. 2006, 642: 5-10.1016/j.physletb.2006.08.074.
Zimdahl W, Pavon D: Phys Rev D. 2000, 61: 108301-10.1103/PhysRevD.61.108301.
Pegoraro F, Radicati LA, Bernard Ph, Picasso E: Phys Lett A. 1978, 68: 165-10.1016/0375-9601(78)90792-2.
Reece CE, Reiner PJ, Melissinos AC: Nucl Inst and Methods. 1986, A245: 299-10.1016/0168-9002(86)91263-5.
Reece CE, Reiner PJ, Melissinos AC: Phys Lett. 1984, 104A: 341-
Bernard P, Gemme G, Parodi R, Picasso E: Rev Sci Instrum. 2001, 72: 2428-10.1063/1.1366636.
Ballantini R, Bernard P, Chincarini A, Gemme G, Parodi R, Picasso E: Class Quant Grav. 2004, 21: S1241-10.1088/0264-9381/21/5/127.
Cruise AM: Class Quantum Grav. 2000, 17: 2525-10.1088/0264-9381/17/13/305.
Cruise AM, Ingley RM: Class Quantum Grav. 2005, 22 (10): S479-10.1088/0264-9381/22/10/046.
Cruise AM, Ingley RM: Class Quantum Grav. 2006, 23: 6185-10.1088/0264-9381/23/22/007.
Li FY, Tang MX, Shi DP: Phys Rev D. 2003, 67: 104008-10.1103/PhysRevD.67.104008.
Nishizawa A, et al: Phys Rev D. 2008, 77: 022002-10.1103/PhysRevD.77.022002.
Montroy TE, et al: Astrophys J. 2006, 647: 813-10.1086/505560.
Wu JHP, et al: Astrophys J. 2007, 665: 55-10.1086/518112.
Johnson BR, et al: Astophys J. 2007, 665: 42-10.1086/518105.
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Giovannini, M. Stochastic backgrounds of relic gravitons: a theoretical appraisal. PMC Phys A 4, 1 (2010). https://doi.org/10.1186/1754-0410-4-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1754-0410-4-1









 denotes indifferently either
denotes indifferently either 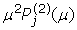 ;
; ;
;






