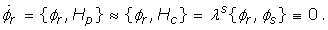- Research article
- Open access
- Published:
Quantum cosmology of a classically constrained nonsingular Universe
PMC Physics A volume 3, Article number: 5 (2009)
Abstract
The quantum cosmological version of a nonsingular Universe presented by Mukhanov and Brandenberger in the early nineties has been developed and the Hamilton Jacobi equation has been found under semiclassical (WKB) approximation. It has been pointed out that, parameterization of classical trajectories with semiclassical time parameter, for such a classically constrained system, is a nontrivial task and requires Lagrangian formulation rather than the Hamiltonian formalism.
PACS Codes: 98.80.Qc, 04.50.Kd.
1 Introduction
It transpires from Hawking-Penrose energy condition that the singularities of the general theory of relativity are unavoidable classically. In the absence of a complete and satisfactory theory of quantum gravity, it is not clear what would be the nature or the fate of singularities in the quantum domain. However, it might be possible in principle to get rid of the singularities classically by imposing some quantum mechanical bounds on certain quantities. At the singularity, some of the curvatures, eg., energy momentum and even the Riemann tensors diverge. Further, quantum field theory predicts that, the scattering cross sections become infinity when all radiative corrections are taken into account. Renormalization makes individual terms manageable, but the entire series diverges. So in order to get rid of the singularities, curvature invariant terms must be constrained to take some upper limits. If Planck's length l
pl
is assumed to be the fundamental length, below which no length is measurable, then from dimensional argument, curvature invariants must be bounded as,  , etc. However, curvature invariants are infinite in number and there is no guarantee that imposing constraint on some lower order curvature invariant terms, all the higher order terms will be bounded. Hence, 'Limiting Curvature Hypothesis' (LCH) [1] had been invoked. LCH states that a finite number of curvature invariants should be bounded and one of those, say I2, should have the property that I2 = 0 singles out a particular nonsingular solution as the only one. In the process all the infinite set of curvature invariants are automatically bounded. If the limiting space is de-Sitter, then for a isotropic Universe, LCH implies that the initial and the final stages of cosmological evolution for a closed Universe will give de-Sitter phase, while baby Universes will arise at the centre of the Black-Hole and eventually gravitational collapse is avoided.
, etc. However, curvature invariants are infinite in number and there is no guarantee that imposing constraint on some lower order curvature invariant terms, all the higher order terms will be bounded. Hence, 'Limiting Curvature Hypothesis' (LCH) [1] had been invoked. LCH states that a finite number of curvature invariants should be bounded and one of those, say I2, should have the property that I2 = 0 singles out a particular nonsingular solution as the only one. In the process all the infinite set of curvature invariants are automatically bounded. If the limiting space is de-Sitter, then for a isotropic Universe, LCH implies that the initial and the final stages of cosmological evolution for a closed Universe will give de-Sitter phase, while baby Universes will arise at the centre of the Black-Hole and eventually gravitational collapse is avoided.
Since Weyl tensor vanishes for an isotropic Universe, so in its simplest form, LCH can be realized by constraining only a couple of lower order curvature invariants, viz., I1 = 4R and  . Thus in its simplest form, ie., for homogeneous and isotropic space-time, Mukhanov and Brandenberger [2] followed by Brandenberger, Mukhanov and Sornborger [3] had constructed the following action (1), which preserves LCH.
. Thus in its simplest form, ie., for homogeneous and isotropic space-time, Mukhanov and Brandenberger [2] followed by Brandenberger, Mukhanov and Sornborger [3] had constructed the following action (1), which preserves LCH.

Here, the scalar field ϕ2 has been introduced to obtain nonsingular solutions, while ϕ1 bounds the curvature invariants for these nonsingular solutions. The potentials V1(ϕ1) and V2(ϕ2) should be chosen in a manner such that (i) for ϕ i ≪ 1, the leading terms in the action gives back Einstein's theory and (ii) their asymptotic behaviour should be such that LCH may be realized, which requires V1(ϕ1) → constant as ϕ1→ ∞, and V2(ϕ2) → 0 as ϕ2 → ∞. For a at Robertson-Walker metric, they ([2] &[3]) had obtained a first order differential equation containing fields and the potentials and had drawn a phase diagram in ϕ1-ϕ2 plane, for some particular choice of the potentials. The phase diagram indicates nonsingular solutions in all regions and de-Sitter phase in the asymptotic region. In a nut-shell, the results obtained [4] are the following. Firstly, all the homogeneous and isotropic cosmological solutions are nonsingular. Next, Two dimensional cosmological and Black-Hole solutions are nonsingular. Such Black-Hole solutions in particular, exhibit Schwarzchild solution at large radial co-ordinate and never evaporate completely [5]. Finally, there are evidence that nonsingular solutions may exist for four-dimensional Black-Holes and homogeneous-anisotropic cosmological models. Further, LCH has also been applied to dilaton-cosmology [6, 7] and as a result, a class of spacially flat bouncing cosmological solutions have emerged. This construction is definitely appealing in itself, however, it also incorporates some additional features in quantum domain. In the path integral formulation of quantum gravity, one has to analytically continue the Lorentzian space of indefinite metric to the Euclidean space of positive definite metric in order to ensure convergence of the path integral. Nevertheless, since Euclidean action of the gravitational field is not bounded from below, the path integral never really converges. The action presented by Mukhanov and Brandenberger [2] and Brandenberger, Mukhanov and Sornborger [3] is bounded from below, and therefore, the corresponding path integral converges. In addition, since the initial and the final stages of cosmological evolution are de-Sitter, so one gets Lorentzian wormholes instead of Euclidean. Finally, as the authors had claimed that the theory can incorporate matter field and also can be extended to include anisotropic models, so it appears that the model is of greater interest with a wide spectrum of its applicability.
In the theory under consideration, two scalar fields, one of which is non-dynamical, have been nonminimally coupled to gravity, containing higher order curvature invariant term. Thus, along with the lapse function N(t), an additional Lagrange multiplier is required in connection with the non-dynamical Scalar field, leading to classically constrained gravity theory. Study of Quantum cosmological aspects of such a constrained theory may reveal more important cosmological implications. eg., in a recent work, such an attempt was made by Gabadadze and Shang [8] for a different classically constrained theory of gravity, which has been found to admit solutions, absent from general theory of relativity. However, the new solutions have some wonderful features like,-the spatially flat de-Sitter Universe can be created from nothing, has boundaries, with vanishing total energy, etc. [9]. So, it appears worth to study the quantum cosmological aspects of the theory under consideration. Therefore, the constrained Hamiltonian dynamics of the theory under consideration has been studied along the line of Dirac's algorithm to find a constraint free primary Hamiltonian. Despite the fact that the theory under consideration contains constraints in addition to the Hamiltonian constraint of the standard theory of gravity, no attempt has been made to find the true degrees of freedom and to find the expression for the Hamiltonian in the reduced phase space. Rather, it has been quantized in the same tune of Wheeler-deWitt equation,  |Ψ > = 0. However, since the only justification for a quantized method lies in its success, so the corresponding semiclassical approximation has been treated here explicitly.
|Ψ > = 0. However, since the only justification for a quantized method lies in its success, so the corresponding semiclassical approximation has been treated here explicitly.
The main motivation of this work is to study the connection of the quantum-cosmological equations for the theory under investigation with the Hamilton-Jacobi equations of the classical theory and in the process to point out the difficulty in finding the semiclassical time required to parameterize classical trajectories. It has been observed that it is nontrivial task to extract semiclassical time parameter for such a constrained system. It has been shown that the semiclassical time parameter extracted in the usual manner does not lead to classical constraint equation. Further, the semiclassical time parameter may be found through speculation, but it is complex and requires Wick rotation. It has also been shown that in order to parameterize classical trajectories by an unique real time parameter, it is required to analyze Lagrangian constrained dynamics rather than Hamiltonian.
In the following section we have written down the classical field equations corresponding to the action under consideration for isotropic and homogeneous Robertson-Walker space time. The Hamiltonian and the corresponding Wheeler-deWitt equation have been found in section 3, after analyzing the constraint of the theory. Semiclassical approximation has been made by expressing the wave function as,  , and then by expanding S in the powers of M instead of ħ. In the process, Hamilton-Jacobi equation has been found in section 4. In section 5, the usual procedure to extract the semiclassical time parameter has been attempted. However, it fails to fulfill the basic requirement of reproducing classical (Hamiltonian) constraint equation. Other naive techniques to find the time parameter have also been explored. Section 6 is devoted to follow an involved technique to find the unique semiclassical time parameter, which is the main motivation of the present paper. In section 7, a source term has been incorporated in the action and the same procedure has been followed. In the process, the functional Schrödinger equation has been found and the uniqueness of the semiclassical time parameter has been proved without ambiguity. The outcome of the present work has been summarized in section (8). Finally, we have added up an appendix in section 9, to remind the readers about the semiclassical approximation in quantum cosmology.
, and then by expanding S in the powers of M instead of ħ. In the process, Hamilton-Jacobi equation has been found in section 4. In section 5, the usual procedure to extract the semiclassical time parameter has been attempted. However, it fails to fulfill the basic requirement of reproducing classical (Hamiltonian) constraint equation. Other naive techniques to find the time parameter have also been explored. Section 6 is devoted to follow an involved technique to find the unique semiclassical time parameter, which is the main motivation of the present paper. In section 7, a source term has been incorporated in the action and the same procedure has been followed. In the process, the functional Schrödinger equation has been found and the uniqueness of the semiclassical time parameter has been proved without ambiguity. The outcome of the present work has been summarized in section (8). Finally, we have added up an appendix in section 9, to remind the readers about the semiclassical approximation in quantum cosmology.
2 Formalism
The action presented by Mukhanov and Brandenberger [2], corresponding to a homogeneous and isotropic non-singular Universe, for which Weyl tensor vanishes, is given by,

where, V1(ϕ1) and V2(ϕ2) are the potentials corresponding to the pair of apparently non-dynamical scalar fields ϕ1 and ϕ2 respectively. LCH may be realized from the above action (1), only for some appropriate choice of the potentials. Action (1) leads to Einstein's theory at small curvature, provided, V
i
(ϕ
i
) ~  , at |ϕ
i
| ≪ 1, where, i = 1, 2. Further, to realize LCH, first requirement is to bound the curvature and the next is to obtain nonsingular solutions. Curvature is bounded provided, V1(ϕ1) ~ ϕ1 at |ϕ1| ≫ 1 and de Sitter solution is obtained in the asymptotic region, provided, V2(ϕ2) ~ constant, at |ϕ2| ≫ 1.
, at |ϕ
i
| ≪ 1, where, i = 1, 2. Further, to realize LCH, first requirement is to bound the curvature and the next is to obtain nonsingular solutions. Curvature is bounded provided, V1(ϕ1) ~ ϕ1 at |ϕ1| ≫ 1 and de Sitter solution is obtained in the asymptotic region, provided, V2(ϕ2) ~ constant, at |ϕ2| ≫ 1.
Now, taking Robertson-Walker line element,

where N(t) is the lapse function, the Ricci scalar is given by,

and the next higher order curvature invariant term is,

So the action takes the following form,

where, the surface term is

 , being the trace of the extrinsic curvature. The surface term is clearly different from the one that appears in Einstein-Hilbert action. However, the two are the same, if ϕ2 vanishes, which has got a kinetic term in the action, and acts as a dynamical variable. It is important to notice that the surface term is not affected by the presence of the scalar field ϕ1, since it acts as Lagrange multiplier only. In the above action N and ϕ1 act as Lagrange multipliers, resulting in a pair of constraint equations. Variation with respect to N gives the Hamiltonian constraint equation, but one can fix the gauge, N = 1, without loss of generality. However, we are not going to fix the other Lagrange multiplier ϕ1, since it has been invoked to bound the curvature invariants for the nonsingular universe guaranteed by the field variable ϕ2. So, altogether we get four equations (not all independent), two of which are constraint equations and those obtained under the variation with respect to ϕ2 and the scale factor a are the two field equations, where we set, N = 1, at the end. The constraint equation appearing under the variation of ϕ1 is,
, being the trace of the extrinsic curvature. The surface term is clearly different from the one that appears in Einstein-Hilbert action. However, the two are the same, if ϕ2 vanishes, which has got a kinetic term in the action, and acts as a dynamical variable. It is important to notice that the surface term is not affected by the presence of the scalar field ϕ1, since it acts as Lagrange multiplier only. In the above action N and ϕ1 act as Lagrange multipliers, resulting in a pair of constraint equations. Variation with respect to N gives the Hamiltonian constraint equation, but one can fix the gauge, N = 1, without loss of generality. However, we are not going to fix the other Lagrange multiplier ϕ1, since it has been invoked to bound the curvature invariants for the nonsingular universe guaranteed by the field variable ϕ2. So, altogether we get four equations (not all independent), two of which are constraint equations and those obtained under the variation with respect to ϕ2 and the scale factor a are the two field equations, where we set, N = 1, at the end. The constraint equation appearing under the variation of ϕ1 is,

while the ϕ2 variation equation is,

The Hamiltonian constraint equation, obtained by varying the action (3) with respect to N is,

Finally, varying the action with respect to the scale factor a, one gets,

In the above field equations  and
and  denote the derivatives of the potentials with respect to ϕ1 and ϕ2 respectively. For spatially flat, k = 0 case, the above field equations can be combined to yield a first order differential equation,
denote the derivatives of the potentials with respect to ϕ1 and ϕ2 respectively. For spatially flat, k = 0 case, the above field equations can be combined to yield a first order differential equation,

The phase diagram for a particular choice of the potentials was plotted by Mukhanov and Brandenberger [2], showing four different classes of trajectories. In the first, the trajectory starts from the de-Sitter phase as ϕ2 → - ∞ and evolves through to de-Sitter as ϕ2 → ∞. In the second, for small initial values of ϕ1 trajectory starts at ϕ2 = -∞ reaches a turning point and returns to ϕ2 = -∞. In the third, the trajectory shows periodic solutions about Minkowski space-time ϕ1 = ϕ2 = 0. Finally, in the fourth class, trajectories starting with small ϕ1 and  , along with ϕ2 ≥ 0, evolve towards de-Sitter at ϕ2 = ∞. In a nutshell, all the phase trajectories are either periodic about Minkowski space-time or else they asymptotically approach to de Sitter space. Hence all solutions are nonsingular. It is important to note that if
, along with ϕ2 ≥ 0, evolve towards de-Sitter at ϕ2 = ∞. In a nutshell, all the phase trajectories are either periodic about Minkowski space-time or else they asymptotically approach to de Sitter space. Hence all solutions are nonsingular. It is important to note that if  vanishes, ϕ2 turns out to be a constant and as a result
vanishes, ϕ2 turns out to be a constant and as a result  vanishes and the resulting solutions again become singular. However, the condition
vanishes and the resulting solutions again become singular. However, the condition  > 0 is satisfied by all the potentials chosen by Mukhanov and Brandenberger [2].
> 0 is satisfied by all the potentials chosen by Mukhanov and Brandenberger [2].
3 Analyzing the constraint and the Wheeler-deWitt equation
It is important to note that in the process of developing an action that might produce nonsingular cosmological solutions, the determinant of the Hessian,  , corresponding to the Lagrangian of the above action (3) vanishes, and so the action becomes singular. Vanishing of the determinant of Hessian, signals the presence of constraint in the theory which should be analyzed step by step carefully. Dirac algorithm [10] is the best known technique to handle such constrained system and to construct the Hamiltonian. Before we proceed, let us recapitulate a few important artefact of Dirac's algorithm.
, corresponding to the Lagrangian of the above action (3) vanishes, and so the action becomes singular. Vanishing of the determinant of Hessian, signals the presence of constraint in the theory which should be analyzed step by step carefully. Dirac algorithm [10] is the best known technique to handle such constrained system and to construct the Hamiltonian. Before we proceed, let us recapitulate a few important artefact of Dirac's algorithm.
1. Firstly we remember that the existence of an infinite invariance group leads to first class constraints, while singular Lagrangians which do not possess a local gauge invariance leads to second class constraints.
2. The rank of W
ij
for a system having 2 N phase space variables (that does not contain time explicitly) is N. For a singular Lagrangian it is R <N. under this circumstances there exists a non-degenerate R × R matrix W
αa
, such that  can be solved for
can be solved for  as
as  , where, a → 1, ...., R, ρ → R + 1, ...., N. In the process one finds, r = N - R primary constraints, p
r
= g
r
(q, p
α
), which originate from the definition of momentum.
, where, a → 1, ...., R, ρ → R + 1, ...., N. In the process one finds, r = N - R primary constraints, p
r
= g
r
(q, p
α
), which originate from the definition of momentum.
3. Now if a function F(q, p) be defined on the primary phase space (this will be defined shortly) Γ p < Γ, then the restriction on F to Γ p is achieved by replacing p r by g r (q, p α ). If F vanishes identically after this replacement, then it is called weakly vanishing and is denoted by F ≈ 0. If in addition the gradient of F also vanishes, then it is called strongly vanishing and is denoted by F ≃ 0.
4. Primary constraints are expressed as ϕ r (q, p) ≈ 0; and the constrained Hamiltonian, defined on the constrained phase space Γ c , as,

One can write down the primary Hamiltonian defined on the primary phase space Γ p , as,

where, λrare the Lagrange multipliers.
-
5.
Next one has to check if the constraints are preserved in time, i.e.,
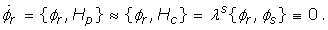
If the Poisson bracket of a constraint vanishes with all other at least weakly, then it turns out to be first class constraint. In that case, {ϕ j , H c } ≈ 0, and all these first class constraints are exhausted. The constraints ϕ i which do not vanish modulo the constraint, leads to secondary constraints χ k .
-
6.
One needs to check the consistency condition of the secondary constraints again, i.e., if the constraints are preserved in time. Again for the secondary constraints, if the poisson brackets of some (say l), vanish with all other, then they are first class and for them {χ l , H c } ≈ 0. Otherwise they are second class in nature and the Lagrange multipliers are determined in the process. There are as many undetermined Lagrange multipliers as there are first class primary constraints. If all the constraints are second class then the primary Hamiltonian together with the primary and secondary constraints constitute the field equations, which may be solved in principle, leaving no arbitrariness in the solutions.
-
7.
Finally, one can try to find the true degrees of freedom and express the Hamiltonian in the reduced phase space Γ R . However, it is a very difficult tusk, if not impossible in most of the situations. Even without finding the reduced Hamiltonian it is possible to quantize the theory. There is no unique prescription in this regard. Any quantum theory may be considered to be the correct one if it can go over to the classical counterpart through a suitable correspondence principle.
With this background knowledge, let us proceed to construct the Hamiltonian of the theory. We understand that in order to construct the primary Hamiltonian, one has to introduce all the constraints of the theory in the Hamiltonian through Lagrange multiplier. Choosing  = M, M being the square of the Planck mass, one finds in view of the action (3) under the gauge choice N = 1,
= M, M being the square of the Planck mass, one finds in view of the action (3) under the gauge choice N = 1,

while  is not invertible due to the constraint,
is not invertible due to the constraint,

Since,  , so the above constraint vanishes weakly. Hence the primary Hamiltonian may be expressed as,
, so the above constraint vanishes weakly. Hence the primary Hamiltonian may be expressed as,

where, α is the Lagrange multiplier. Since, {C1, H c } does not vanish even weakly, so C1 is a second class primary constraint. As there are no first class primary constraint, so there will be no undetermined Lagrange multiplier of the theory. Now the constraint must be preserved in time, i.e.,

This is a new second class constraint as long as  exits, since {C1,
exits, since {C1,  } = {C1, D1} =
} = {C1, D1} =  . As already pointed out that for the existence of nonsingular solutions
. As already pointed out that for the existence of nonsingular solutions  must not vanish, here we again observe that
must not vanish, here we again observe that  must not vanish to remove arbitrariness from the primary Hamiltonian. However no such restriction is required for V2. Again the condition that the constraint should be preserved in time leads to,
must not vanish to remove arbitrariness from the primary Hamiltonian. However no such restriction is required for V2. Again the condition that the constraint should be preserved in time leads to,

modulo the constraint (10). This is not a new constraint, rather it fixes the Lagrange multiplier  provided
provided  exists. Thus both the primary and the secondary constraints are second class. Hence the primary Hamiltonian, being free from arbitrariness can now be expressed as,
exists. Thus both the primary and the secondary constraints are second class. Hence the primary Hamiltonian, being free from arbitrariness can now be expressed as,

One can now easily check that we have obtained the correct Hamiltonian in the usual manner. The only exception appears to be with  , which looks like a new equation. However, this is the one, we were in search of, since ϕ1 can now be inverted through this equation. In any case, it is not an independent equation, since taking time derivative of the first (constraint) equation (4) and using the second one (5), one can arrive at it. Thus the Hamiltonian, (12) being free from constraints and being able to produce all the field equations, is the correct one. To make a comparison, let us take Einstein-Hilbert action minimally coupled to a scalar field,
, which looks like a new equation. However, this is the one, we were in search of, since ϕ1 can now be inverted through this equation. In any case, it is not an independent equation, since taking time derivative of the first (constraint) equation (4) and using the second one (5), one can arrive at it. Thus the Hamiltonian, (12) being free from constraints and being able to produce all the field equations, is the correct one. To make a comparison, let us take Einstein-Hilbert action minimally coupled to a scalar field,

and write down the corresponding Hamiltonian,

It is interesting to note that the classical field equations (4) through (7) reduce to the vacuum Einstein's equations at any stage of cosmic evolution as ϕ1 = ϕ2 = 0. However, the primary Hamiltonian (12) once constructed in view of the constrained system under investigation, is different from (13) and does not ever reduce to the vacuum Einstein's equation. This fact has been manifested in the linear appearance of p a in Hp1. The fact that here p a appears linearly in the Hamiltonian, clearly differentiates all actions (corresponding to minimal and standard non-minimal coupling) with the present one.
Our next attempt will be to canonically quantize the theory under consideration. There is no standard prescription to quantize a classically constrained system and the only justification of a particular method of quantization lies in its success. The meaning of the last sentence is that one should be able to find a correspondence principle to go over to the classical theory under semiclassical limit. We shall write down the counterpart of the Wheeler-deWitt equation  |Ψ > = 0, for the modified theory of gravity under consideration and show in the following sections how to find the notion of semiclassical time so that classical field equations may be reproduced. Now, in constructing the Wheeler-deWitt equation corresponding to the Hamiltonian (12), operator ordering ambiguities should be taken care off. Some of the operator ordering ambiguities may be removed by expressing,
|Ψ > = 0, for the modified theory of gravity under consideration and show in the following sections how to find the notion of semiclassical time so that classical field equations may be reproduced. Now, in constructing the Wheeler-deWitt equation corresponding to the Hamiltonian (12), operator ordering ambiguities should be taken care off. Some of the operator ordering ambiguities may be removed by expressing,  where, q(a) is an arbitrary function of a. Hence the first term of the Wheeler-deWitt equation corresponding to the Hamiltonian (12), after replacing
where, q(a) is an arbitrary function of a. Hence the first term of the Wheeler-deWitt equation corresponding to the Hamiltonian (12), after replacing  by -i ħ▽, turns out to be
by -i ħ▽, turns out to be

Clearly, first order derivative of the wavefunction Ψ with respect to a, (ie.,  ) does not appear, while the same with respect to the scalar field (ie.,
) does not appear, while the same with respect to the scalar field (ie.,  ) appears. Further, operator ordering in
) appears. Further, operator ordering in  and
and  appearing due to the presence of the second and the third terms in (12), again introduces first derivative terms (ie.,
appearing due to the presence of the second and the third terms in (12), again introduces first derivative terms (ie.,  and
and  ) in the Wheeler-deWitt equation, corresponding to the scalars ϕ
i
. However, from the regularity argument [11], it follows that
) in the Wheeler-deWitt equation, corresponding to the scalars ϕ
i
. However, from the regularity argument [11], it follows that  can be neglected at sufficiently small values of a, ie, at sufficiently early epoch. Hence, the Wheeler-deWitt equation may be kept free from the first derivative terms even after removing some of the operator ordering ambiguities (unlike the situation encountered in standard and other nonstandard theories of gravity), and is expressed as,
can be neglected at sufficiently small values of a, ie, at sufficiently early epoch. Hence, the Wheeler-deWitt equation may be kept free from the first derivative terms even after removing some of the operator ordering ambiguities (unlike the situation encountered in standard and other nonstandard theories of gravity), and is expressed as,

which is independent of the operator ordering parameter q(a). Not all quantum states |Ψ > of the Wheeler -deWitt equation (14) are allowed, since they are constrained by the quantum analogue of the classical constraints (10) and (11). However, since our aim is not to find the solution of (14), so we neither, are in search of true degrees of freedom nor incorporate the quantum analogue of the classical constraints. Rather, for the sake of comparison, we write down the Wheeler-deWitt equation corresponding to Einstein's gravity with a minimally coupled scalar field (see Appendix),

where, q takes care of some of the operator ordering ambiguities. We observe that, neither  nor
nor  term appears in the Wheeler-deWitt equation (14), which may have some deep significance, not presently known.
term appears in the Wheeler-deWitt equation (14), which may have some deep significance, not presently known.
4 Semiclasical approximation
Reparametrization invariance of the theory of gravity leads to the Hamiltonian constraint yielding Wheeler-deWitt equation. Despite the fact that the theory under consideration has additional constraints, we have not made any attempt to find the true degrees of freedom to construct the Hamiltonian in the reduced phase space Γ
R
. Rather, the corresponding quantum equation (14) has been constructed in the same tune of the standard Wheeler-deWitt equation  |Ψ > = 0. Now the obvious question is, "does equation (14) alone represents the quantum version of the classical field equations (4) through (7)"? Other way round one may ask, "is it possible to set up a correspondence between the Wheeler-deWitt equation (14) and the classical equations (4) through (7)"?. Since, the constraint free Hamiltonian represents the correct one to reproduce all the classical field equations, so the answer to the question raised above is positive, if under a suitable semiclassical prescription, one can find a semiclassical notion of time to recover the Hamilton constraint equation (6) from the Wheeler-deWitt equation (14). It is a nontrivial task which we shall take up in this and in the following sections.
|Ψ > = 0. Now the obvious question is, "does equation (14) alone represents the quantum version of the classical field equations (4) through (7)"? Other way round one may ask, "is it possible to set up a correspondence between the Wheeler-deWitt equation (14) and the classical equations (4) through (7)"?. Since, the constraint free Hamiltonian represents the correct one to reproduce all the classical field equations, so the answer to the question raised above is positive, if under a suitable semiclassical prescription, one can find a semiclassical notion of time to recover the Hamilton constraint equation (6) from the Wheeler-deWitt equation (14). It is a nontrivial task which we shall take up in this and in the following sections.
At energy below Planck scale, the wave function can be expressed as,  . Expanding, S in the powers of M as, S = MS0 + S1 + M-1S2 + ⋯, and inserting it in the Wheeler-deWitt equation (14), one obtains
. Expanding, S in the powers of M as, S = MS0 + S1 + M-1S2 + ⋯, and inserting it in the Wheeler-deWitt equation (14), one obtains

Let us now collect expression having same powers in M. For Einstein-Hilbert action with minimally coupled fields one gets to the power of M2 an expression that states that the Hamilton-Jacobi function S0 depends on three space only (see Appendix). Here the situation is quite different in the sense that we do not get expressions corresponding to the order M2. To the order M1, we have,

This is the Hamilton-Jacobi equation. It can be identified with the Hamiltonian constraint equation (6) only under an appropriate choice of semiclassical time parameter. Following two sections are devoted to find the semiclassical time parameter.
5 Semiclassical time parameter - standard technique
Since in view of the Hamiltonian (12) all the velocities are now invertible and so following standard technique as in Einstein's gravity with minimally coupled scalar field (see Appendix, 9.2), the time parameter can be found as,

The problem is that, this choice of time parameter does not lead to classical constraint equation (6). This is because,  appearing in the Hamilton-Jacobi equation (16) is not obtainable from it and as a result, remains arbitrary. This is the source of trouble that we encounter in the present situation, to parameterize classical trajectories with semiclassical time parameter following usual procedure. Thus, the standard procedure does not work in the classically constrained system under consideration.
appearing in the Hamilton-Jacobi equation (16) is not obtainable from it and as a result, remains arbitrary. This is the source of trouble that we encounter in the present situation, to parameterize classical trajectories with semiclassical time parameter following usual procedure. Thus, the standard procedure does not work in the classically constrained system under consideration.
One can try to find the same by expressing the time parameter as

where, b, c, d, j, l, m, u, v and n are arbitrary functions of a, ϕ1 and ϕ2. It is now possible to find  and
and  , using this expression as,
, using this expression as,

Substituting all these expressions in equation (6) and equating the coefficients of ▽S0 etc., between the equation thus formed and the Hamilton-Jacobi equation (16), one can finally arrive at the following time parameter,

With this technique of parametrization, classical constraint equation (6) is automatically reproduced, but the problem associated with this time parameter is that, there still exists an arbitrariness in the form of the arbitrary parameter n = n(a, ϕ1, ϕ2). Thus, the time parameter is not unique, and something else should be tried.
It is interesting to note that simply by inspection one can choose a time parameter free from such arbitrariness as,

This time parameter reproduces equation (6), in view of Hamilton-Jacobi equation (16). However, this is purely intuitive on one hand and is imaginary on the other. So we must find an involved technique for this purpose.
6 Semiclassical time parameter - an involved technique
As already mentioned, equation (4) is an additional gravitational constraint equation of the theory under consideration, since it does not contain second order derivatives. The standard technique should be to differentiate equation (4) and then to compare it with equation (6). In the process, if the emerging equation is again a constraint equation, then it should be entered into the Lagrangian via Lagrange multiplier. The emerging constraint equation in this case is,

Hence, introducing this constraint equation (17) in action (3) via a Lagrange multiplier λ, we obtain,

The canonical momenta are found from the action (18) as,

We don't write down the field equations since we are not going for classical solutions. However, it is important to note that since variation with respect to λ gives back the constraint equation (17) and in view of (19) the classical constraint equation (6) remains unchanged, so, the primary Hamiltonian (12), the Wheeler-deWitt equation (14) and the Hamilton-Jacobi equation (16) are systematically reproduced. Further, identifying canonical momenta with corresponding derivatives of the Hamilton-Jacobi function, equation (12) can be found again from Hamilton-Jacobi equation (16). Now in order to obtain equation (6) from (16), let us use equations (17) and (19), which gives,



Equations (20), (21) and (22) are now combined to yield the correct and unique semiclassical time parameter,

One can now easily obtain  ,
,  and
and  from above time parameter (23) and substituting these in equation (16), one can reproduce equation (6). To check whether we have found the correct and unique semiclassical time parameter let us continue by including a source term (in the form of a dynamical scalar field) in the model.
from above time parameter (23) and substituting these in equation (16), one can reproduce equation (6). To check whether we have found the correct and unique semiclassical time parameter let us continue by including a source term (in the form of a dynamical scalar field) in the model.
7 Including a source term
In this section we consider an additional source term in the action (1), in the form of a minimally coupled scalar field with Lagrangian density,

where, σ is the scalar field and U(σ) is an arbitrary potential. The action (1) now reads (taking  , as before),
, as before),

Corresponding field equations are (under variation of the above action with respect to ϕ1, ϕ2, σ, N and a and setting N = 1),





where,  ,
,  and {U'(σ) are the derivatives of the potentials with respect to ϕ1, ϕ2 and σ respectively. As before we differentiate equation (25) with respect to time and compare it with equation (26) to get the constraint equation
and {U'(σ) are the derivatives of the potentials with respect to ϕ1, ϕ2 and σ respectively. As before we differentiate equation (25) with respect to time and compare it with equation (26) to get the constraint equation

Next we incorporate this equation (30) into the Lagrangian through the same Lagrange multiplier λ, as before. In view of the Lagrangian so formed, we obtain the same set of canonical momenta (19) along with an additional one, corresponding to the field σ, viz.,

Variation of the Lagrangian with respect to the Lagrange multiplier λ returns equation (30). So, in view of equations (19), (30) and (31), one can express all the velocities in terms of momenta, and thus the primary Hamiltonian free from arbitrariness of Lagrange multiplier is found as,

Corresponding Wheeler-deWitt equation  |Ψ > = 0 is,
|Ψ > = 0 is,

As before, we proceed to make semiclassical approximation by expressing Ψ[a, ϕ1, ϕ2, σ] as  expanding S in power series of M as, S = MS0 +S1 +M-1S2 + ⋯ etc., and then substituting all these in equation (33). Finally, equating terms having different orders of M to zero, we find for M2 order
expanding S in power series of M as, S = MS0 +S1 +M-1S2 + ⋯ etc., and then substituting all these in equation (33). Finally, equating terms having different orders of M to zero, we find for M2 order

M1 order term leads to Hamilton-Jacobi equation for the source free nonsingular gravitational field as,

One can easily identify this equation with the Hamilton-Jacobi equation (16). It leads to the classical source free gravitational constraint equation (6) under the same choice of the time parameter (23). Hence, source free Hamiltonian (12) can be found from it by identifying the canonical momenta with corresponding derivatives of S0, as before. The next, ie., M0 order term gives the following equation,

Now in order to identify this equation (36) with the functional Schrödinger equation for the matter field σ, let us define a function,

In view of (37), equation (36) reduces to

provided, the function D(a, ϕ i ) satisfies the following equation,

Since the right hand side of equation (38) is the quantum Hamiltonian operator for the scalar field σ operating on function f, in the background of curved space time, so it is clear that equation (38) is the functional Schrödinger equation for the field σ, propagating in the background of curved space time, under the same choice of the time parameter (23). Further, under the same choice of time parameter (23), equation (39) reduces to,

Hence, upto this order of approximation, we have,

where, S0 is obtainable from equation (35), f from (38) and D from (39) or (40). So at the end we observe that under the same choice of time parameter (23), one can parameterize the classical trajectories by reproducing classical source free gravitational equation (6) from the source free Hamilton-Jacobi equation (35) at one hand, while the M0 order term (36) can be identified with the functional Schrödinger equation (38) for the field σ propagating in the background of curved space time, on the other. This time parametrization is unique since equation (38) reduces to the functional Schrödinger equation only under the choice of the real time parameter (23) leaving no arbitrariness. This choice is correct since it fulfills both the requirements of obtaining functional Schrödinger equation and parametrization of the classical trajectories.
8 Concluding remarks
In a series of works, Brandenberger, Mukhanov, Sornborger and others [2–4] and [6] constructed a nonsingular gravitational action by invoking limiting curvature hypothesis (LCH) and studied its classical aspects. The action contains a couple of scalar fields, one of which (ϕ2) is required to guarantee nonsingular solutions, while the other (ϕ1) binds the curvature invariants. The corresponding potentials are chosen in such a manner that for |ϕ i | ≪ 1, Einstein's theory is recovered at one hand and their asymptotic behaviour should be such that LCH may be realized on the other. In the present work, we have studied the quantum cosmological aspect of the theory and made a connection of the quantum cosmological equation with the Hamilton-Jacobi equation of the classical theory. The answer to the question that, why it is at all necessary to quantize a nonsingular Universe model, lies in fact that some new results have been unveiled in the process and a non-trivial technique of parameterizing the classical trajectories has been found. Summarily, the results are,
1.) Introduction of the scalar field ϕ1 in the action (1), only introduces yet another constraint equation (other than the Hamiltonian constraint). Thus it is essentially a classically constrained theory of gravity and so one has to deal with such constraints critically, which we have done using Dirac's algorithm.
2.) In the absence of the scalar fields, the classical field equations reduce to those corresponding to standard theory of gravity. However, the Hamiltonian obtained after analyzing the constraint, does not give Einstein's theory back. Likewise, the Wheeler-deWitt equation is free from first derivative terms  , and thus is quite different from those obtained in view of standard and other nonstandard (nonminimally coupled) theories of gravity.
, and thus is quite different from those obtained in view of standard and other nonstandard (nonminimally coupled) theories of gravity.
3.) The wave function is real for k = ± 1, unlike the situation encountered in standard gravity theory (see appendix), where, k = +1 leads to a complex wave function.
4.) The semiclassical time parameter required to parameterize classical trajectories can be found in a unique way only by using the technique of Lagrange undetermined multiplier in the Lagrangian constrained dynamics, rather than using Hamiltonian formalism.
9 Appendix
Paramerizing Einstein's gravity with a minimally coupled scalar field with semiclassical time
In the appendix we shall recapitulate the standard technique [12–14], to parameterize classical trajectories of the Hamilton-Jacobi equation, with some appropriate choice of semiclassical time parameter, corresponding to Einstein's gravity with a minimally coupled scalar field, and to find the functional Schrödinger equation. The action for Einstein's gravity with a source term - a minimally coupled scalar field ϕ, (with  , which is different from
, which is different from  , used in the text) is,
, used in the text) is,

apart from a surface term. The  component of Einstein's equation is
component of Einstein's equation is

which corresponds to the Hamilton constraint equation,

Thus, the corresponding Wheeler-deWitt equation is

where, p takes care of some of the operator ordering ambiguities.
9.1 Expansion with power series of Planck's constant ħ
In the standard WKB approximation, the wave functional Ψ is expressed as  and the functional S(a, ϕ) is expanded in the power series of the Planck's constant ħ as, S = S0 + ħ S1 + ħ2S2 + ⋯ etc. Substituting all these in the Wheeler-deWitt equation (44), and collecting terms independent of ħ, one obtains,
and the functional S(a, ϕ) is expanded in the power series of the Planck's constant ħ as, S = S0 + ħ S1 + ħ2S2 + ⋯ etc. Substituting all these in the Wheeler-deWitt equation (44), and collecting terms independent of ħ, one obtains,

This is Einstein-Hamilton-Jacobi (EHJ) equation, which is essentially equation (43), if one identifies p
a
with  and p ϕ with
and p ϕ with  . In order to parameterize classical trajectories, WKB time parameter is chosen in the following manner,
. In order to parameterize classical trajectories, WKB time parameter is chosen in the following manner,

and

The classical trajectories are parameterized by a time, which is a linear combination of (46) and (47). Thus,

Under this choice of time parameter (48), equation (45) produces Einstein's equation (42). This has been shown by Kiefer [12], taking, a = exp α and using the unit M = 1. It is important to note that the choice of the semiclassical time parameter does not involve operator ordering ambiguity. Equation (45) can in principle be solved for S0 and to this order of approximation one obtains  . Higher order terms of ħ produce fluctuations around the classical trajectory S0 and hence introduce corrections to the wave-functional Ψ.
. Higher order terms of ħ produce fluctuations around the classical trajectory S0 and hence introduce corrections to the wave-functional Ψ.
9.2 Expansion with power series of Planck's mass M
In the present work, we have expanded S(a, ϕ) in the power series of Planck's mass, instead. The advantage is that, one can obtain a functional Schrödinger equation directly from it. Substituting, S = MS0 + S1 + M-1S2 + ⋯ etc., in the Wheeler-deWitt equation (44) and collecting terms in different orders in M, we obtain for M2 order,  = 0. It implies that S0 is purely a functional of gravitational field. M1order term gives the source free Einstein-Hamilton-Jacobi (EHJ) equation,
= 0. It implies that S0 is purely a functional of gravitational field. M1order term gives the source free Einstein-Hamilton-Jacobi (EHJ) equation,

Now, in the absence of the matter field, equations (42) and (43) reduce to

respectively. Hence the EHJ equation (49) is essentially the vacuum Einstein equation (50), under the identification  . To parameterize classical trajectories, we identify,
. To parameterize classical trajectories, we identify,

Further in view of equation (49), we have,

Under the choice of the time parameter (52), equation (49) reduces to the vacuum Einstein's equation (50). Hence, expansion of S in the power series of M decouples gravity from the source and leaves it to behave classically. Equation (49) can be solved for S0, and up to this order of approximation,

Thus the wave-functional is well behaved at the classical singularity a → 0. The next order of approximation yields the following equation,

where, p takes care of some of the factor ordering ambiguities. Now choosing a function,  and substituting
and substituting  and
and  from it in the above equation (54), one obtains,
from it in the above equation (54), one obtains,

provided, D(a) satisfies the following equation,

Equation (55) can be identified with Tomonaga-Schwinger equation, which is essentially the functional Schrödinger equation for the mater field propagating in the background of curved space-time, if the semi-classical time operator is identified with (51). The right hand side of equation (55) represents quantum Hamilton operator  for the matter field operating on the function f(a, ϕ). Thus equation (55) reduces to
for the matter field operating on the function f(a, ϕ). Thus equation (55) reduces to

Equation (56) can be solved for D(a) as,

Substituting  , in equation (56), one obtains,
, in equation (56), one obtains,

m being the constant of integration. Finally, to this order of approximation, the wave-functional takes the form,

Equation (55) can in principle be solved for f(a, ϕ) and thus explicit form of the wave-functional can be obtained. Now to make semiclassical approximation to the functional Schrödinger equation (55), let us express  , expand A in the power series of ħ as, A(a, ϕ) = A0 + ħ A1 + ħ2A2+ ⋯, substitute it in equation (55) and collect terms independent of ħ, to get,
, expand A in the power series of ħ as, A(a, ϕ) = A0 + ħ A1 + ħ2A2+ ⋯, substitute it in equation (55) and collect terms independent of ħ, to get,

Since we have already identified  with the semiclassical time parameter
with the semiclassical time parameter  , in equation (52), so the above equation takes the form,
, in equation (52), so the above equation takes the form,

Further, if one identifies  with p
ϕ
, it transpires that equation (62) is the Hamiltonian for the matter field in the background of curved space time, corresponding to the classical action,
with p
ϕ
, it transpires that equation (62) is the Hamiltonian for the matter field in the background of curved space time, corresponding to the classical action,  in the isotropic and homogeneous space-time under consideration. Now, since
in the isotropic and homogeneous space-time under consideration. Now, since  , so
, so

and the suppressed part of the WKB time parameter appearing in equation (48) reappears. This when combined with equation (51), one finally obtains the semiclassical time parameter as,

References
Frolov VP, Markov MA, Mukhanov VF: Phys Rev. 1990, D41: 383-
Mukhanov V, Brandengerger R: Phys Rev Lett. 1992, 68: 1969-10.1103/PhysRevLett.68.1969.
Brandenberger R, Mukhanov V, Sornborger A: Phys Rev. 1993, D48: 1629-
Brandenberger R: gr-qc/9509059
Damien A Easson: JHEP. 2003, 0302: 037-hep-th/0210016
Brandenberger R, Easther R, Maia JMF: JHEP. 1998, 9808: 007-10.1088/1126-6708/1998/08/007. gr-qc/9806111
Easson Damien, Brandenberger R: JHEP. 1999, 9909: 003-10.1088/1126-6708/1999/09/003. hep-th/9905175
Gabadadze G, Shang Y: hep-th/0506040
Gabadadze G, Shang Y: Phys Lett. 2006, B635: 235-
Sundermeyer K: Constrained dynamics, Lecture Notes in Physics. 1982, Springer-Verlag, Newyork
del Campo S, Vilenkin A: Phys Rev. 1989, D40: 688-
Kiefer C: Class Quant Gravit. 1987, 4: 1369-10.1088/0264-9381/4/5/031.
Padmanabhan T: IJMPA. 1989, 4: 4735-4818. 10.1142/S0217751X89002004.
Padmanabhan T, Singh TP: Class Quant Gravit. 1990, 7: 411-10.1088/0264-9381/7/3/015.
Acknowledgements
I would like to thank prof. R. Brandenberger and the reviewers for going through the manuscript and rendering some valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Sanyal, A.K. Quantum cosmology of a classically constrained nonsingular Universe. PMC Phys A 3, 5 (2009). https://doi.org/10.1186/1754-0410-3-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1754-0410-3-5